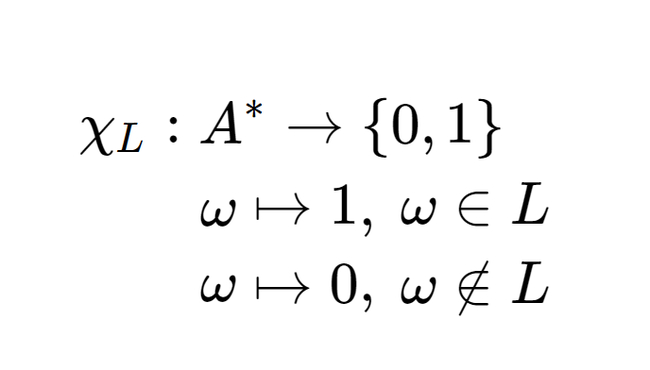Два фермера собрали урожай фруктов, причём второй собрал на 40% меньше, чем первый?
Математика | 1 — 4 классы
Два фермера собрали урожай фруктов, причём второй собрал на 40% меньше, чем первый.
Среди фруктов, собранных первым фермером, яблоки составляют 22%, а вторым – 70%.
Сколько процентов составляют яблоки среди фруктов, собранных двумя фермерами вместе?
(60 * 0, 22) + (40 * 0, 7) = 41, 2%.
В первый день фермер собрал в своем саду 26 ящиков яблок, а во второй — 14 таких же ящиков яблок?
В первый день фермер собрал в своем саду 26 ящиков яблок, а во второй — 14 таких же ящиков яблок.
Сколько кг яблок собрал фермер в первый день и сколько — во второй, если во второй день он собрал на 192 кг меньше, чем в первый?
Дети собрали в саду груши и яблоки?
Дети собрали в саду груши и яблоки.
Из всех собранных фруктов 30% были груши, а остальные — яблоки.
Из всех собранных яблок 60% — апорт.
Сколько процентов от числа всех собранных фруктов составляет апорт?
Фермеры в своем саду в первый день собрали 4520 кг яблок, а груш – на 2 т 635 кг меньше?
Фермеры в своем саду в первый день собрали 4520 кг яблок, а груш – на 2 т 635 кг меньше.
За второй день собрали яблок 3 т 18 кг, а груш – на1 т 6 ц 78 кг больше, чем яблок.
Сколько всего фруктов собрали фермеры?
Фермеры в своем саду в первый день собрали 4520 кг яблок, а груш на 2 т 635 кг меньше?
Фермеры в своем саду в первый день собрали 4520 кг яблок, а груш на 2 т 635 кг меньше.
За второй день собрали яблок 3 т 18 кг, а груш на 1 т 6 ц 78 кг больше, чем яблок.
Сколько всего фруктов собрали фермеры?
Дети собрали в саду груши и яблоки?
Дети собрали в саду груши и яблоки.
Из всех собранных фруктов 30% были груши, а остальное яблоки.
Из всех собранных яблок 60% апорт.
Сколько процентов от числа всех собранных фруктов составляет апорт ?
Дети собрали в саду груши и яблоки?
Дети собрали в саду груши и яблоки.
Из всех собранных фруктов 30% были груши а остальные яблоки.
Извсех собранных яблок 60% сколько процентов от числа всех собранных фруктов составляет апорт.
Дети собрали в саду груши и яблоки?
Дети собрали в саду груши и яблоки.
Из всех собранных фруктов 30% были груши, а остальные — яблоки.
Их всех собранных яблок 60% — апорт.
Сколько процентов от числа всех собранных фруктов составляет апорт?
Фермер собрал урожай яблок у груш?
Фермер собрал урожай яблок у груш.
При этом яблок собрал на 328кг меньше , чем груш.
Сколько кг груш собрал фермер, если их было в 3 раза больше чем яблок?
За три дня фермеры собрали 4638 кг яблок?
За три дня фермеры собрали 4638 кг яблок.
В первый день они собрали 1 / 3 часть всех яблок.
Сколько кг яблок собрали фермеры в третий день .
Если в первый было собрано на 684 кг меньше.
Чем во в второй.
Дети собирали в саду яблоки и груши?
Дети собирали в саду яблоки и груши.
Из всех собранных фруктов 30% были груши, остальные яблоки.
Из всех собранных яблок 60% — апорт.
Сколько процентов от всех собранных фруктов составляет апорт?
Вопрос Два фермера собрали урожай фруктов, причём второй собрал на 40% меньше, чем первый?, расположенный на этой странице сайта, относится к категории Математика и соответствует программе для 1 — 4 классов. Если ответ не удовлетворяет в полной мере, найдите с помощью автоматического поиска похожие вопросы, из этой же категории, или сформулируйте вопрос по-своему. Для этого ключевые фразы введите в строку поиска, нажав на кнопку, расположенную вверху страницы. Воспользуйтесь также подсказками посетителей, оставившими комментарии под вопросом.
M увеличили на 25%, значит получилось m + 1 / 4m потом (1, 1 / 4m) * 0. 2 = 0. 25m m уменьшилось на 4 раза.
M * 1. 25 после первого увеличения 1, 25m * 0. 8 = m число не изменилось.
Второй это не четные числа.
(1)5. 039684199579492 (2)12. 59921049894873.
B = 0. (100 — 0) — 10 = 90 получится.
1)b = 0 100 — 0 = 100 100 — 10 = 90 2) b = 2 100 — 2 = 98 98 — 10 = 88 3) b = 10 100 — 10 = 90 90 — 10 = 80 4) b = 30 100 — 30 = 70 70 — 10 = 60.
Цена за кг : 1) 105 : 350 * 1000 = 300 руб 2) 40 : 120 * 1000 = 333 руб 33 коп 3) 39 : 130 * 1000 = 300 руб 4) 184 : 800 * 1000 = 230 руб В упаковке 800 г продается печенье по наименьшей цене за килограмм.
1) 15 — 8 = 7 (м) — стоят 756 руб 2)756 : 7 = 108(руб) — стоит 1 молоток ответ : 108 рублей удачи в школе ! ))).
Решение задания смотри на фотографии.
(15 * 2) + (5 * 2) = 30 + 10 = 40(км)велосипедисты удалятся друг от друга за 2 ч Ответ : 40км.
Источник
2 фермера собрали урожай фруктов
У фермера есть два поля, каждое площадью 15 гектаров. На каждом поле можно выращивать картофель и свёклу, поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет 400 ц/га, а на втором — 300 ц/га. Урожайность свёклы на первом поле составляет 250 ц/га, а на втором — 400 ц/га.
Фермер может продавать картофель по цене 2000 руб. за центнер, а свёклу — по цене 3000 руб. за центнер. Какой наибольший доход может получить фермер?
Заметим, что на первом поле с одного гектара можно собрать либо 400 центнеров картофеля и получить 12 000 000 рублей, либо 250 центнеров свёклы и получить 11 250 000 рублей. Таким образом, нужно всё первое поле отдать под картофель. На втором поле с одного гектара можно собрать либо 300 центнеров картофеля и получить 9 000 000 рублей, либо 400 центнеров свёклы и получить 18 000 000 рублей. Поэтому второе поле нужно целиком отдать под свёклу. В этом случае фермер сможет заработать 15 · 400 · 2000 + 15 · 400 · 3000 = 30 000 000 (рублей).
Ответ: 30 млн рублей.
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ | 2 |
| Верно построена математическая модель | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Аналоги к заданию № 513292: 513296 515785 517184 517222 Все
Источник
Задача про фермера по математике
Пока карантин учитель дал всем в классе задание пройти математический конкурс, который проводит факультет математики местного универа.
Чтоб было проще проверять я для себя прорешал задачки. Благо 5-ый класс я еще могу осилить 🙂
Заинтересовала вот эта задача:
Заинтересовала тем, что я ее решил составив систему уравнений с двумя неизвестными.
Уравнения не сложные. Решить легко. Одно неизвестное выразил из второго, подставил , посчитал, подставил обратно — готово. Мешок моркови = 20 кг, гороха = 15 кг.
НО они в 5-м классе еще НЕ проходили уравнения с двумя неизвестными.
Думаю нафига такое давать детям, придется опять за учителя работать, объяснить суть таких уравнений, чтобы у нее получилось решить.
Открыл задание на этой задаче, позвал дочь и говорю вот попробуй решить задачку, а я пока в душ схожу. Потом выйду объясню.
Возвращаюсь через 5 минут, а дочка говорит что решила. Дает ответ 100 кг. — правильно, у меня также получилось.
Удивляюсь. Не ожидал. Думал она составит эти уравнения и дальше дело у нее не пойдет, а тут правильный ответ. Я ее дольше решал.
Спрашиваю: «Когда вы системы уравнений успели пройти?» — она вообще не в курсе что это такое 🙂 и показывает решение. А там все до гениального просто. Нужно только быть внимательным при прочтении условия задачи.
В условии пункт «А). 3 мешка моркови и 2 куля гороха весят столько же, сколько 9 мешков картофеля«. Потом говорится, что «Один мешок картошки весит 10 килограмм«
И сам вопрос «Сколько килограмм вместе весят 3 мешка моркови, 2 куля гороха и 1 мешок картошки?«
У меня в голове сразу уравнения начали складываться, а не затуманенный этой белибердой детский мозг увидел, что там все проще простого.
Дочь говорит: «Смотри в пункте А) сказано все тоже самое, что и нужно узнать, только + еще 1 мешок картошки, который тоже дано сколько весит» .
ВСЕ, для решения задачи данные пункта Б) даже не нужны
1 мешок картошки = 10 кг. по условию, а 3 мешка моркови и 2 гороха весят как 9 мешков картошки = 90 кг. опять таки по условию пункта А).
Просто и гениально.
Сказал что будет свой вариант решения писать, а не эти непонятные уравнения.
Дети и родители
5.3K постов 9.6K подписчиков
Правила сообщества
1.Соблюдать правила Пикабу
2.Не стоит выкладывать посты по типу «мы пописали» «мы поели» «это наш первый зуб»
3.Не устраивать споры и срачи по каждому не похожему на ваше мнение
4.Ставить нормальные тэги.
5.Нельзя выкладывать посты не по теме сообщества.
6. Поддерживать интересных авторов
Сказал что будет свой вариант решения писать, а не эти непонятные уравнения.
И правильно сделает. Потому что за решение способом, который не проходили может (зависит от учителя) двойку получить. Уже сколько случаев упоминалось.
«У меня в голове сразу уравнения начали складываться, а не затуманенный этой белибердой детский мозг увидел, что там все проще простого.» — уравнения это белиберда?
Ну да, действительно.
1. Задача повышенной сложности, как я понял. На смекалку.
2. Как раз решить уравнениями можно ЛЮБУЮ подобную задачу. А вот смекалкой — только эту конкретную, под конкретное условие.
Это два абсолютно разных действия. Конкретная задача на смекалку для 5-го класса и классическая система уравнений с двумя неизвестными, которая позволяет решить любую такую задачу.
Вы просто сравниваете теплое и твердое, что неправильно.
Дети в третьем классе решали задачи: Петя и Вася поймали на двоих 15 рыб, но Вася поймал в два раза больше Пети. Сколько поймал каждый? Ну, думаю, показывайте, как будете выкручиваться.
Решали так: Вместе поймали 3 части, две части уходит Вася, одна Пете. 15:3=5. 5 рыб у Пети, 10 у Васи.
Еще одна: Петя и Вася поймали 15 рыб, но Вася поймал на 3 рыбы больше. Сколько у каждого?
3 рыбы это разница между уловом мальчиков, надо ее убрать. 15-3=12. 12 рыб у них на двоих одинаково. Получается у Пети 6 рыб, у Васи 9.
Потом на эти задачи усложнялись, дополнялись, но смысл тот же.
По-моему в пятом классе мы бы просто умножили первое всё на два и за разницей со вторым выражением получили бы что мешок моркови весит как два мешка картошки. Ну а дальше уже считаешь горох и общую сумму.
Не пойму, почему вы считаете что дети с системой уравнений не справятся без помощи.
У меня в голове сразу уравнения начали складываться, а не затуманенный этой белибердой детский мозг увидел, что там все проще простого.
Похоже на то, что вы считаете, будто учёба в старших классах «затуманивает мозг белибердой». Но на самом деле, чем больше вы решаете таких систем и вообще разных задач, тем быстрее замечаете, где можно упростить. В данном случае сразу понятно, что уравнение б) вовсе не нужно.
Я вот чего-то вспоминаю и не могу вспомнить, были ли в моём школьном детстве задачи с подобными отвлекающими, но не нужными для решения, условиями. А в современных школьных заданиях, такое ощущение, что это чуть ли не обязательно.
Как и большинство не заметил простой ответ через пункт А). Я толком не прочёл вопрос кинулся искать неизвестные. Даже не составляя системы уравнений, вывожу, что если из а рвого удвоенного условия вычесть второе, то получаем что 1 мешок моркови весит 2 мешка картошки. А один куль гороха полтора мешка. Ну а найдя все неизвестные стал разбираться, а что же я собственно ищу.
Я уже блеать блокнот достал и начал уравнения писать. Сцук, как полезен порой свежий незамыленный взгляд на задачу. Все гениальное просто, нехуй велосипеды изобретать.
В 5 классе не знают как решать системы уравнений?
Мой в первом классе их как орешки щелкает.
вы не поверите, но математика это один большой способ найти решение проще, изящней, но что бы видеть это простое и изящное решение, нужно знать все способы(
Фига вы уверенный в себе 🙂 Нашли один способ решения и прям сразу возмущение, что не по возрасту задача. Даже в голову не пришло, что ошиблись или недосмотрели где-то.
Только меня смутил «фермер по математике»? ТС, с русским тоже не очень.
Гимназист VII класса Егор Зиберов милостиво подает Пете Удодову руку. Петя, двенадцатилетний мальчуган в сером костюмчике, пухлый и краснощекий, с маленьким лбом и щетинистыми волосами, расшаркивается и лезет в шкап за тетрадками. Занятие начинается.
Согласно условию, заключенному с отцом Удодовым, Зиберов должен заниматься с Петей по два часа ежедневно, за что и получает шесть рублей в месяц. Готовит он его во II класс гимназии. (В прошлом году он готовил его в I класс, но Петя порезался.)
— Ну-с. — начинает Зиберов, закуривая папиросу. — Вам задано четвертое склонение. Склоняйте fructus!
Петя начинает склонять.
— Опять вы не выучили! — говорит Зиберов, вставая. — В шестой раз задаю вам четвертое склонение, и вы ни в зуб толконуть! Когда же, наконец, вы начнете учить уроки?
— Опять не выучил? — слышится за дверями кашляющий голос, и в комнату входит Петин папаша, отставной губернский секретарь Удодов. — Опять? Почему же ты не выучил? Ах ты, свинья, свинья! Верите ли, Егор Алексеич? Ведь и вчерась порол!
И, тяжело вздохнув, Удодов садится около сына и засматривает в истрепанного Кюнера. Зиберов начинает экзаменовать Петю при отце. Пусть глупый отец узнает, как глуп его сын! Гимназист входит в экзаменаторский азарт, ненавидит, презирает маленького краснощекого тупицу, готов побить его. Ему даже досадно делается, когда мальчуган отвечает впопад — так опротивел ему этот Петя!
— Вы даже второго склонения не знаете! Не знаете вы и первого! Вот вы как учитесь! Ну, скажите мне, как будет звательный падеж от meus filius 1?
— От meus filius? Meus filius будет. это будет.
Петя долго глядит в потолок, долго шевелит губами, но не дает ответа.
— А как будет дательный множественного от dea 2?
— Deabus. filiabus! — отчеканивает Петя.
Старик Удодов одобрительно кивает головой. Гимназист, не ожидавший удачного ответа, чувствует досаду.
— А еще какое существительное имеет в дательном abus? — спрашивает он.
Оказывается, что и «anima — душа» имеет в дательном abus, чего нет в Кюнере.
— Звучный язык латинский! — замечает Удодов. — Алон. трон. бонус. антропос. Премудрость! И всё ведь это нужно! — говорит он со вздохом.
«Мешает, скотина, заниматься. — думает Зиберов. — Сидит над душой тут и надзирает. Терпеть не могу контроля!» — Ну-с, — обращается он к Пете. — К следующему разу по латыни возьмете то же самое. Теперь по арифметике. Берите доску. Какая следующая задача?
Петя плюет на доску и стирает рукавом. Учитель берет задачник и диктует:
— «Купец купил 138 арш. черного и синего сукна за 540 руб. Спрашивается, сколько аршин купил он того и другого, если синее стоило 5 руб. за аршин, а черное 3 руб.?» Повторите задачу.
Петя повторяет задачу и тотчас же, ни слова не говоря, начинает делить 540 на 138.
— Для чего же это вы делите? Постойте! Впрочем, так. продолжайте. Остаток получается? Здесь не может быть остатка. Дайте-ка я разделю!
Зиберов делит, получает 3 с остатком и быстро стирает.
«Странно. — думает он, ероша волосы и краснея. — Как же она решается? Гм. Это задача на неопределенные уравнения, а вовсе не арифметическая».
Учитель глядит в ответы и видит 75 и 63.
«Гм. странно. Сложить 5 и 3, а потом делить 540 на 8? Так, что ли? Нет, не то».
— Решайте же! — говорит он Пете.
— Ну, чего думаешь? Задача-то ведь пустяковая! — говорит Удодов Пете. — Экий ты дурак, братец! Решите уж вы ему, Егор Алексеич.
Егор Алексеич берет в руки грифель и начинает решать. Он заикается, краснеет, бледнеет.
— Эта задача, собственно говоря, алгебраическая, — говорит он. — Ее с иксом и игреком решить можно. Впрочем, можно и так решить. Я, вот, разделил. понимаете? Теперь, вот, надо вычесть. понимаете? Или, вот что. Решите мне эту задачу сами к завтраму. Подумайте.
Петя ехидно улыбается. Удодов тоже улыбается. Оба они понимают замешательство учителя. Ученик VII класса еще пуще конфузится, встает и начинает ходить из угла в угол.
— И без алгебры решить можно, — говорит Удодов, протягивая руку к счетам и вздыхая. — Вот, извольте видеть.
Он щелкает на счетах, и у него получается 75 и 63, что и нужно было.
— Вот-с. по-нашему, по-неученому.
Учителю становится нестерпимо жутко. С замиранием сердца поглядывает он на часы и видит, что до конца урока остается еще час с четвертью — целая вечность!
После диктанта — география, за географией — закон божий, потом русский язык, — много на этом свете наук! Но вот, наконец, кончается двухчасовой урок. Зиберов берется за шапку, милостиво подает Пете руку и прощается с Удодовым.
— Не можете ли вы сегодня дать мне немного денег? — просит он робко. — Завтра мне нужно взносить плату за учение. Вы должны мне за шесть месяцев.
— Я? Ах, да, да. — бормочет Удодов, не глядя на Зиберова. — С удовольствием! Только у меня сейчас нету, а я вам через недельку. или через две.
Зиберов соглашается и, надев свои тяжелые, грязные калоши, идет на другой урок.
Могу предложить вам забрать дочь из школы чтобы ее мозг оставался таким же чистым и не затуманенным этой белибердой с уравнениями
Взрыв потенциальной энергии: звонок он для учителя
Прочел ответ @Khabkron #comment_219865874 вспомнил как у нас было.
Сидим на уроке, классная конкретно отчитывает за то, что мы 9-й класс, а все еще носимся как бешенные. А еще вылетаем из класса как только звонок прозвучит. Говорит: звонок он не для вас, он для учителя. Вот когда дам разрешение, тогда и можете идти.
Натерпелись ее наставлений. Звучит звонок.
Мы ждем. Через 3 секунды классная: можете идти.
Мы всем классом вылетаем с криком «ааааААААаа» в дверь ибо вода скоро начнет водить. Выносим дверь с петель, кто-то падает на дверь, давка. Через 5 секунд осознаем, что выбили закрытую на ключ вдерь (видать училка решила подстраховаться и закрыла дверь чтобы никто не выбежал полсе звонка, а открыть забыла).
Потом на собрании не знаю что было, но дверь починили.
Путь в школу
Пермская учительница закрыла собой учеников от нападавших. Интервью с Наталией Шагулиной
Это произошло в 2018 году в первую неделю после зимних каникул. В обычную школу в Перми вошли два подростка с ножами. Они ворвались в кабинет 4-го класса и начали наносить удары всем без разбора: и учительнице, и детям.
Учительница Наталия Шагулина получила 17 ножевых ранений, но сумела защитить своих учеников и вывести их из класса. Все пострадавшие выжили, хотя и провели в больнице несколько месяцев.
Обычно после таких случаев на всех каналах начинают разбирать и анализировать произошедшее. Наталия Шагулина не давала интервью и не бывала на ток-шоу, посвящённых школьному буллингу, его последствиям и другим больным темам. Но она согласилась принять участие в проекте «Подвиги», и с ней записали уникальный подкаст. Слушайте интервью – оно и о том нападении, к которому никто не был готов, и о выздоровлении, и о поддержке друг друга, о награде для Наталии и о наказании для преступников.
Друзья, предваряя возможные вопросы и пожелания на тему «Почему вы в посте всё сразу не напишете?», скажу: о Наталии мы писали много: и посты, и на своём сайте, и главу в книге. А подкаст – это новый формат для нас, а для вас – возможность послушать голос героя.
Во Владикавказе росгвардейцы спасли детей из охваченной огнем школы
Спасены более 500 детей, благодаря оперативным действиям никто не пострадал💪
Про гуманитария, математику и репетитора
Довелось учиться в позднем СССР/перестройку. В школе отставала по математике.
С ней была просто беда. Так, как по остальным предметам училась хорошо, математику мне «натягивали». Но в выпускном классе математику стала вести молодая амбициозная преподавательница, которая ставила то, что заслужил.
Итог: мне грозила двойка по математике и справка вместо аттестата.
Моя мать подсуетилась и наняла мне преподавательницу из технического ВУЗа. Очень приятную женщину в возрасте, еврейку. Таких мягких и очаровательных людей я редко встречала в жизни. С первого же урока я начала что-то понимать. Каждый урок шел буквально за год. Встречи были как праздник.
Контрольную годовую я написала на 5, и, одна единственная в классе, верно решила дополнительное задание. Учителя не понимали: я у кого-то списала? Но у кого, ведь никто не решил дополнительное задание!
Много лет мучительных страданий и всего несколько уроков у талантливого педагога.
Жизненная ситуация
На что собирают деньги в американской школе и про младшешкольное образование в целом
Осенний семестр подходит к концу и самое время написать пару слов о школе.
Начать наверное стоит с того что система американских школы выглядит запутанной по сравнению с российскими 1-11 класс.
В Америке обязательное обучение начинается с K — kindergarten (прямо перевода детски сад, но это уже не сад все таки) . В K дети идут с 5 лет и это обязательно отдавать ребёнка в K, но до K есть ещё pre-K для детей с 4 лет, который не обязателен, но там как бы готовят детей к школе, плюс это помощь родителям в плане что не нужно платить за садик. В разных штатах по разному но в Нью-Йорке часы pre-K с 8 до 2.20, можно оставлять ребёнка и до 6 вечера, но тогда нужно доплачивать.
До pre-k есть ещё 3-K, он тоже бесплатный, там по-моему часы с 8 до 4 дня, но эту программу сделали только несколько лет назад, поэтому мы на неё не попали, но смысл похожий бесплатная программа для 3 леток в больших детских садах, то есть детскому саду за неё платит город.
В Pre-k 4 леток знакомят с буквами и цифрами, учат писать своё имя и теоретически к K они уже приходят немножко подготовленные, но там конечно все равно заново проходят с детям алфавит, учат первые слова, писать коротенькие предложения и конечно писать. К концу учебного года ожидается что 5 летний ребёнок может написать коротенькое предложение типа I see my cat, my cat is black. И читать тексты похожего уровня. И впринципе на слух они уже могут писать многие слова, но понятно что с ошибками.
В начале года я ожидала список вещей которые нужно купить для школы, всякие там карандаши, фломастеры, листочки. Купила кое какие карандаши и так что то по мелочи. Сосисок так и не пришёл, сказала что в этом году школа полностью обеспечит детей всеми этими принадлежностями. Рюкзак тоже выдали, но ребёнок конечно захотел свой, а школьный используем для походов на кружки. Спросила учительницу не нужно ли купить какие то детям штучки типа наклеек, маленьких поощрительных «призов» которые обычно дают детям за хорошо сделаные задания, она сказала что этого ничего не надо, все есть.
Формы у нас нет, поэтому такой статьи расходов к школе как форма тоже нет.
Да, на начало учебного года не принято ничего дарить учителю вы ведь не собираетесь его подкупить таким образом), даже цветы, хотя русскоговорящие детки иногда приходят с цветами, думаю учителям все равно приятно получить букетик. Нашей учительнице тоже подарили пару букетов. Есть день Благодарности учителю когда принято дарить подарки, но не большие, стандартная цена на такой подарок не превышает $25, для сравнения минимальная оплата труда $15 в час. Также некоторые дарят подарки учителю на Рождество, чаще всего что то с праздничное, типа конфеты или красивую игрушку на ёлку.
Телефоны, телевизоры и прочее не дарят ни на какие праздники, это я сейчас вспомнила свой выпускной)
Никаких сборов на «парты» и прочей ерунды нет.
Из за пандемии дети сидят на уроках в масках кроме времени принятия пищи, ланч можно приносить с собой, можно брать в школе. Школьный ланч бесплатный, но по-моему самое съедобное что там дают это яблоко, морковку и молоко. Остальное это малосьедобные бургеры на ватном хлебе, или странные вещи типа тортильяс с соусом сальса, печеньки или крекеры, салат из зелёных листьев. Ребёнок из любопытства в начале года взял пару ланчей, откусил и остаток приносил домой, это реально малосьедобно. Завтрак тоже дают бесплатно, там вроде дают обычно хлопья с молоком. Короче полезного питания там не много, но есть те семьи где родители не парятся о том что ест ребёнок, поэтому спасибо хоть в школе кормят.
На праздники детям иногда устраивают какие то развлечения типа сбор тыкв на Хэллуин и дальнейших их дизайн) на тыквы деньги не собирали это было организовано от школы. Но на праздничный стол на День Благодарения чтобы дети тоже сделали себе праздничный ланч сказали принести фрукты или овощи или сладости на класс.
На что собирали деньги так это на фото, каждый год делают что типа школьного альбома и там можно выбрать разные опции, базовая была что то около $20 и там можно заказать кучу ерунды с фото ребёнка типа: кружки, брелки, сумки и прочее.
Также в этом году из ковида школа не предоставляет программу продлённого дня, а обычно она была, в некоторых школах бесплатная, в некоторых за денежку, стоит это что то около $200 в месяц насколько я слывшая от подруги. В нашей школе вроде раньше было бесплатно, в этом году ее нет в любом случае. Также обычно школы закрыты на лето, но в связи с пандемией чтобы финансово помочь родителям сделали бесплатные летние лагеря на территории школы, это не прям летние лагеря конечно где дети совершают какие то увлекательные поездки итд, но просто тем куда некуда девать детей можно было хотя бы оставлять ребёнка на целый день под присмотром.
Обычно в школах есть всякие кружки для детей, но для этого возраста ничего не предлагалась нам в этом году, а может и из за пандемии, посмотрим что будет дальше.
Тем кто далеко живёт от школы бесплатно представляется школьный автобус, также как детям с инвалидностью, но так как мы живем близко нам не пришлось воспользоваться такой услугой от школы.
Вот наверно пока и все мои впечатления, в целом мне казалось что детям в таком возрасте тяжеловато учиться, по долгу сидеть на одном месте, но ребёнок не жалуется, кажется в саду он больше уставал, но возможно потому что там день был до 6, а в школе только до 2.
Я тебе еще добавлю!
Я чет не пойму, все родители за своих гавнюков заступаются, что бы они не натворили, что в школе на учителей кидаются и везде правы, что дальше во взрослой жизни.
Только мне мои родители, с их родителями говорили, если учитель/воспитатель на тебя пожалуется (отлупит) я тебя защищать не буду, еще и добавлю, что бы вел себя прилично.
Ну логично же ответил
Олимпиада по математике 3 класс
Как я закончил школу с 5-й по инязу
В школе по инязу у меня от роду не было пятерки. Были,кажется, одни четверки и то с натяжками. Единственное что было — это замечание учителей по поводу моего произношеия: тут произнес «о» вместо «эу», а здесь больше «р» вместо «а». И эта ерунда с произношением была всегда. Что в одной школе, что в новой. Я как-то не смотрел на других, пытался свое исправить. А потом стал приглядываться и понял, что не только у меня эти проблемы.
И вот переехал, сменил школу и там продолжилось все то же самое. Как так-то? Может старая школа переправили со мной мою хар-ку по всем предметам?! XD По сути новая училка придиралась к моему произношению. И, как я помню, исключительно из-за произношения у меня была бы 4-ка под конец 11-го класса если бы не районная (а может муждугородняя, не разбираюсь) олимпиада.
И вот, Марья Николаевна объявила в классе новость, сказала что отличники точно поедут, но может и еще кто-то. Никто не захотел кроме меня. Так что меня взяли без вопросов.
Из мелкого городишка приехали в соседний город, началась олимпиада. Она включала несколько этапов: тест, прослушивание аудиозаписи и ответы на вопросы по аудиозаписи. Может еще что-то, не помню, но как-то так.
Прослушали, ответили, вернулись.
Позже пришли результаты: отличники набрали около 160-200 баллов, я под 800 из 1000.
В итоге я все же получил 5-ку от удивленной училки, да и она как-то смотрела после этого на меня странно. Типа как же так?!
Что такое вектор в математике?
Сегодня на занятии мы определим, что такое вектор, каких видов он бывает и разберёмся, как совершать действия с векторами.
Подобные треугольники
Сегодня мы вспомним, что такое подобне треугольники и по каким признакам понять, что они подобны.
История проблемы равенства классов P и NP
В 2000 году Математический институт Клэя определил 7 математических задач, решение которых не могли найти в течение многих лет. За решение каждой из них была назначена награда в размере 1 миллиона долларов. Эти 7 задач известны как «задачи тысячелетия», и на сегодняшний день только одна из них была решена — гипотеза Пуанкаре. В этой статье пойдет речь о вопросе равенства классов P и NP, ответ на который может сильно повлиять на всю IT-сферу.
Равенство P и NP классов отсылает нас к теории алгоритмов, а именно к классам сложности. Первое, с чего стоит начать, это то, что классы P и NP классифицируют языки, а не задачи. Пока что это звучит довольно абсурдно, поэтому для понимания разберемся в некоторых деталях.
В теории алгоритмов алфавит — это непустое конечное множество символов. Набор символов ASCII — это алфавит. <0 , 1>— тоже алфавит. <> — такое множество нельзя назвать алфавитом, поскольку оно пустое, а множество целых чисел Z нельзя назвать алфавитом, поскольку оно бесконечно.
Допустим, мы имеем алфавит. Назовем его A. Тогда словом над алфавитом А является упорядоченное соединение конечного числа символов. Например, 110110 — это слово над алфавитом <0 , 1>, а «habr» — слово над алфавитом ASCII символов. Но число пи не будет словом над алфавитом < . , 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9>, так как число пи из символов данного алфавита не будет конечным. Над любым алфавитом существует пустое слово, обозначать его будем символом e. Слова обладают такой характеристикой, как длина, т. е. количество символов в нем. Обозначать длину слова будем в виде модуля. Длина вышеупомянутого слова |110110| = 6.
Возьмем уже упомянутый алфавит А. Пусть множество А* содержит все слова над алфавитом А, а множество А+ также содержит все слова над А, за исключением e (значки + и * взяты из регулярных выражений). Множество Аn содержит все слова длины n. Для любого алфавита множества А* и А+ будут бесконечными (можно составить бесконечное количество слов разной длины для любого алфавита). Для алфавита А = <0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9>множество А2 будет представлять набор из двузначных чисел.
Пусть А — алфавит и L ⊆ А*, тогда L называется языком над А. Для любого алфавита пустое множество и А* являются тривиальными языками. При этом пустое множество часто называют пустым языком. Однако не стоит путать пустой язык и язык, содержащий пустое слово e, — они различны. Языки могут быть как бесконечными, так и нет, но обязательно счетными. Т. е. множество всех действительных чисел языком нельзя назвать, т. к. такой набор является неисчисляемым.
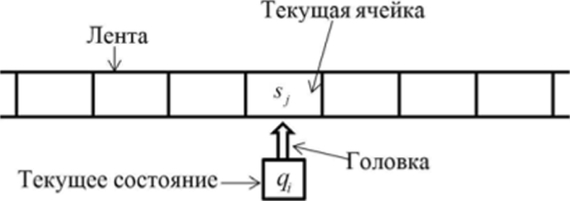
Говоря про абстрактный исполнитель, чаще всего имеют в виду машину Тьюринга, поэтому в дальнейшем под АИ будем подразумевать именно её. Итак, машина Тьюринга имеет неограниченное линейное хранилище, сгруппированное в ячейки. Каждая ячейка может содержать ровно один символ алфавита в любой момент времени. Вдоль ячеек идет считывающая головка, имеющая конечное число состояний. За одну итерацию она может считать значение только одной ячейки, переписать её значение, изменить свое состояние и перейти на одну позицию вправо/влево.
Устройство машины Тьюринга
На основе машины Тьюринга определим так называемую разрешающую машину над языком. Для начала введем определение характеризующей функции X(w). Функция X определяет, принадлежит ли слово w языку L. Если да, то значение функции равно «1»; если нет, то «0». Формально это можно записать так:
Разрешающей машиной D для языка L называется такая машина, которая для каждого w∈A вычисляет характеризующую функцию X(w) за конечное время.
В дополнение к разрешающей машине идет верификатор. Машина V, которая принимает слова w и c и выводит 0 или 1 после конечного числа шагов, называется верификатором для L, если она обладает следующими свойствами:
— выводит 1, только если w входит в язык L;
— для любого w в языке L существует такое c, что V(w,c) = 1.
В данной машине буквой с называется свидетель или сертификат. Фактически, верификатор также проверяет, входит ли какое-либо слово в язык, однако делает это с учетом свидетеля, который ускоряет проверку. Например, возьмем число 182652. Входит ли оно в язык простых чисел, т.е. является ли оно простым. Без компьютера это будет довольно сложно проверить, однако имея сертификат — числа 186 и 982, произведение которых дает в результате число 182652, — задача проверки сильно упрощается. Фактически, свидетель — это любая информация, упрощающая проверку вхождения слова в язык.
Классы сложности и формулировка проблемы
Окей, мы рассмотрели несколько понятий. На первый взгляд, все это больше походит на лингвистику: алфавиты, слова, языки… Причем тут задачи? Чтобы ответить на этот вопрос, обратимся к понятию задача разрешимости (англ. Decision problem). Это такой вопрос (сформулированный в формальной системе), требующий ответа «да» или «нет», зависящего, возможно, от значений некоторых входных параметров. Например, «является ли данное натуральное число x простым?» или «даны два числа: x и y; делится ли x на y?« Метод решения в виде алгоритма называется разрешающей процедурой. Теория вычислимости имеет дело в основном с задачами разрешимости и приведенные выше конструкции наглядно соотносятся с таким типом задач: так разрешающая машина над языком является формализацией разрешающей процедуры. Но как же быть с задачами, такими как задача коммивояжера? На них нельзя дать бинарный ответ. В таких случаях применяют приемы приведения к версии decision problem. В случае коммивояжера проблема по-новому формулируется так: «существует ли маршрут не длиннее, чем заданное значение k?»
В класс сложности NP входят все языки L, для которых существует такой верификатор, что для каждого (w,c) время его работы полиномиально. Иными словами, NP включает в себя задачи разрешимости, для которых при подходящем сертификате для данного w мы быстро сможем удостовериться в том, что w действительно принадлежит L (ответ на вопрос можно довольно быстро проверить). Отсюда и название «верификатор». В качестве примера задачи в NP можно привести определение наличия в графе гамильтонова цикла. Сертификат в данном случае — последовательность вершин, образующих гамильтонов цикл.
Помимо этих классов можно выделить ещё 2: NP-hard и NP-Complete. Они основываются на приводимости одного языка к другому за полиномиальное время: пусть языки A и B — языки над одним алфавитом. Язык А будет приводимым за полиномиальное время к языку B, если существует такая функция f(w), что
— функция f может быть вычислена машиной Тьюринга за полиномиальное время.
Тогда в класс NP-hard будут входить языки, к которым приводимы все языки в NP (причем NP-hard язык может входить в NP, а может и нет), а в NP-Complete те языки, которые являются одновременно NP-hard и NP. Примером NP-Complete является язык выполнимых булевых формул (SAT). Таким образом, NP-Complete задачи образуют в некотором смысле подмножество «типовых» задач в классе NP: если для какой-то из них найден «полиномиально быстрый» алгоритм решения, то и любая другая задача из класса NP может быть решена так же «быстро».
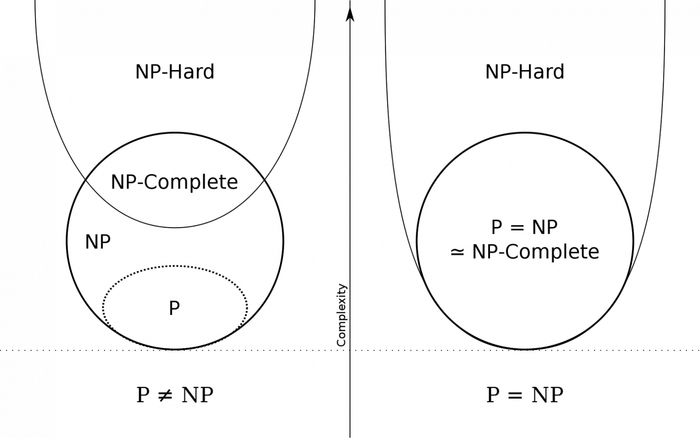
Отношение между классами при равенстве и неравенстве
Теперь, немного погрузившись в теорию алгоритмов, более конкретно обозначим проблему равенства данных классов. Итак, множество P входит в множество NP, но неизвестно, существуют ли языки, которые входят в NP и не входят в P. Что это означает на практике? Итак, простыми словами класс NP можно охарактеризовать как «трудно решить, легко проверить». Классическим примером задачи, входящей в NP, является задача коммивояжера, для решения которой на данный момент известен лишь один алгоритм — старый добрый перебор (мы не рассматриваем эвристические методы). Однако, получив ответ, его будет не так сложно проверить. Класс P же вобрал в себя те задачи, для которых существует эффективный алгоритм решения, позволяющий решать их за полиномиальное время. И равенство или, наоборот, неравенство этих классов пока не доказано. Если эти классы равны, то это будет значить, что для всех задач, которые сейчас решаются путем перебора или другим неэффективным методом, существует(-ют) полиномиальные алгоритмы. А если не равны, то придется смириться с неоптимальностью решения этих задач.
История проблемы равенства P и NP началась в 1928 году, когда Давид Гильберт сформулировал проблему, названную Entscheidungsproblem (нем. задача разрешения). Ее суть заключается в нахождении алгоритма, определяющего доказуемость данного утверждения из аксиом с использованием правил логики. По названию очевидно, что это задача является задачей разрешения (выводит «да» или «нет»).
В ходе решения этой проблемы потребовалось определить термины «алгоритм» и «вычислимая функция». В 1936 году Алонзо Чёрч и Алан Тьюринг независимо показали, что общее решение Entscheidungsproblem невозможно, предположив, что интуитивное понятие «эффективная вычислимость» соответствует вычислимости функции на машине Тьюринга. Эта гипотеза сегодня известна как тезис Чёрча-Тьюринга.
20 марта 1956 в письме к Джону фон Нейману Курт Гёдель впервые поставил вопрос о вычислительной сложности. Гёдель интересовался, можно ли получить доказательство теоремы (в математико-логическом смысле слова) за квадратичное или линейное время. К сожалению, письмо было обнаружено лишь в 1989 году и получило широкую огласку, когда Юрис Хартманис опубликовал перевод и комментарий.
Статья Алана Кобэма 1965 года под названием «The intrinsic computational difficulty of functions» является одним из первых упоминаний класса сложности P, состоящего из разрешимых за полиномиальное время задач. Тезис Кобэма-Эдмондса (известный также как расширенный тезис Чёрча-Тьюринга), названный в честь Алана Кобэма и Джека Эдмондса, утверждает, что любая разумная модель вычислений может быть выражена через другую модель с замедлением, не более чем полиномиальным по размеру входных данных. Кобэм предположил, что класс P может быть хорошим способом для описания множества реально вычислимых задач. Любая проблема, не содержащаяся в P, невозможна, но если задача реального мира может быть решена с помощью алгоритма, существующего в P, то такой алгоритм в конечном итоге будет открыт.
В 1965 году Юрис Хартманис и Ричард Стернс опубликовали статью «On the Computational Complexity of Algorithms», отмеченную премией Тьюринга. В ней даются более точные определения сложности алгоритма и класса сложности. Хартманис и Стернс определили класс сложности как совокупность всех задач, которые можно решить за установленные временные рамки. В их статье показано, что существует бесконечная иерархия классов сложности (например, задачи, для которых наиболее быстрый алгоритм имеет время, пропорциональное n, n log n, n^2, n^3, 2^n и т. д.), где небольшое увеличение временного интервала позволяет решать больше задач. Во второй статье Хартманис совместно с Филипом М. Льюисом показали, что подобная иерархия существует и для количества памяти (функция от размера входа) при решении задачи на машине Тьюринга.
В 1967 году Мануэль Блюм разработал аксиоматическую теорию сложности, которая основана на его собственных аксиомах (аксиомы Блюма), и получил важный результат — теорему об ускорении. До этого мы говорили по большей части о сложности алгоритма. Хотелось бы аналогичным образом определить и сложность задачи: например, какова сложность самого эффективного (по времени и емкости) алгоритма, решающего эту задачу. Теорема об ускорении гласит, что есть некоторые задачи, для которых не существует самого быстрого алгоритма, потому что любой алгоритм для такой задачи можно «ускорить», построив более быстрый алгоритм.
Точная формулировка проблемы равенства P и NP была представлена в 1971 году. Тогда американский ученый Стивен Кук и работавший независимо советский ученый Леонид Левин доказали, что существуют практически актуальные проблемы, которые являются NP-полными. В США Стивен Кук опубликовал статью «The complexity of theorem proving procedures», в которой формализовал понятия редукции за полиномиальное время и NP-полноты, а также доказал существование NP-полной задачи (задача выполнимости булевых формул, SAT). Теорема была независимо доказана Леонидом Левиным и, таким образом, получила название «теорема Кука-Левина».
В 1972 году Ричард Карп сделал рывок в знаменитой статье «Reducibility among Combinatorial Problems», в которой показал, что около 20 разнообразных задач из комбинаторики и теории графов, известных своей вычислительной трудностью, являются NP-полными.
В августе 2010 года Виней Деолаликар, работавший в исследовательском отделении Hewlett-Packard в Пало-Альто в Калифорнии, заявил, что разгадал загадку P vs NP. Он утверждал, что P не равняется NP, однако научное сообщество нашло в его доказательстве фатальную ошибку. В начале 2002 года SIGACT News провел опрос среди 100 ученых, задав им вопрос о равенстве классов NP и P. 61 человек ответили, что «неравны», 9 — «равны», 22 затруднились ответить и 8 сказали, что гипотеза не выводима из текущей системы аксиом и, таким образом, не может быть доказана или опровергнута.
К чему приведет решение проблемы
Окей, теория вычислимости, формализация алгоритмов и абстрактные математические теории — все это конечно интересно, но как решение проблемы равенства NP и P классов отразится на практике? На самом деле, алгоритмы для решения NP-задач используются каждый день во многих сферах. Например, в криптографии, криптовалютах, восстановлении поврежденных файлов, системах блокировки спама, оптимизации в логистике и т. д. Более эффективные решения могли бы значительно сэкономить время и деньги, так как мы пользуемся в основном эвристическими методами, дающими лишь приближенные решения.
Однако существует и обратная сторона монеты. Солидная часть криптографии (криптосистемы с открытым ключом, технологии доказательства выполнения работы в блокчейне, системы блокировки спама) основывается на предположении о неравенстве NP и P классов. Если окажется, что некоторые задачи, для которых, как считалось, не существует эффективных алгоритмов, можно решать быстро, то многие методы защиты устареют.
Может оказаться и так, что последствия решения окажутся не такими тривиальными, как это часто и бывает в математике. В качестве примера рассмотрим континуум-гипотезу о существовании мощности, меньшей континуума и большей мощности счетного множества. Оказывается, существование такого кардинала нельзя ни доказать, ни опровергнуть в аксиоматике ZFC. Так что мы вправе считать, что такие мощности бывают (впрочем, как и считать, что не бывают). Однако ясно, что мы не можем конструктивно построить соответствующее множество. Возможно, точно также окажется и с алгоритмами для NP-задач в случае равенства NP и P (к слову, некоторые математики в опросе SIGACT News так и ответили: гипотеза не выводима из существующей системы аксиом, то есть не может быть доказана или опровергнута).
Пока что существующих методов доказательств недостаточно для строго математического ответа, но не нужно терять надежду. В марте 2001 года Ричард Карп предсказал, что проблема будет решена молодым математиком (до 30 лет) с использованием подхода, о котором еще никто не думал. Стивен Кук заявил, что кто-нибудь предоставит убедительное доказательство в ближайшие 20 лет.
Источник