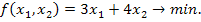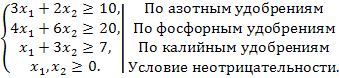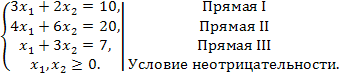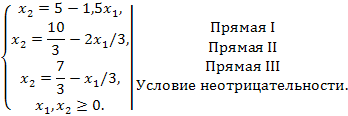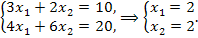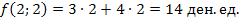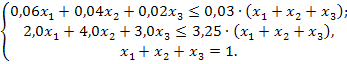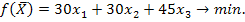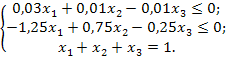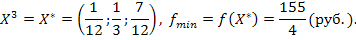Высшая математика все разделы
Образовательные онлайн сервисы: теория и практика
Математическое программирование. Методы оптимизации
Задачи для практической работы
Практическая работа № 1. Составить математические модели задач линейного программирования и привести их к каноническому виду.
Практическая работа № 2. Решить задачи графическим методом.
1. Предприятие электронной промышленности выпускает две модели радиочасов, причем каждая модель производится на отдельной технологической линии. Суточный объем производства первой линии 180 изделий, второй — 200 изделий. На изготовление радиочасов первой модели расходуется 12 однотипных элементов электронных схем I-го вида, 15 — II-го вида, и 8 — III-го вида. На радиочасы второй модели расход деталей соответственно 14, 18 и 6. Максимальный суточный запас используемых элементов I-го вида равен 750 единицам, II-го вида — 700, III-го вида — 800. Прибыль от реализации радиочасов первой и второй модели равна соответственно 25 и 20 ед. Определить оптимальные суточные объемы производства радиочасов первой и второй моделей.
2. Совхоз закупает удобрения двух видов. В единице массы удобрения первого вида содержится 3 ед. фосфора, 8 ед. калия и 6 ед. азота. В единице массы удобрения второго вида этих веществ соответственно 4, 6, 6 единиц. На 1 га почвы необходимо внести не менее 15 ед. фосфора, 12 ед. калия и 15 ед. азота. Составить наиболее экономичный план закупки удобрений, если стоимость одной единицы первого вида удобрений 70 ден. ед., а второго — 80 ден. ед.
Оформление: В электронном виде (Word) .doc
Источник
3 задачи по методам оптимальных решений
| Тема работы: | 3 задачи по методам оптимальных решений |
| Предметная область: | Задачи, Методы принятия оптимальных решений |
| Краткое содержание: | Задание 1. Запишите математическую модель для задачи: Совхоз закупает удобрения двух видов. В единице массы удобрения I вида содержится 3 усл.ед. химического вещества А, 2 усл.ед. – вещества В и 1 усл.ед. вещества С; в единице массы удобрения II вида — 1 усл.ед. химического вещества А, 1 – вещества В и 1 вещества С. На один га почвы необходимо внести не менее 9 усл.ед. вещества А, 8 усл.ед. вещества В и 6 усл.ед. вещества С. Составить наиболее экономичный план закупки удобрений (в расчете на 1 га), если цены удобрений (на 1 ед. массы) таковы: удобрения I вида – 3 ден.ед., II вида – 2 ден.ед. Решить задачу на компьютере. Задание 2. Решить графическим методом задачу линейного программирования. Найти минимум функции при следующих ограничениях: Задание 3. Найти минимум функции при следующих ограничениях: Необходимо: а) решить задачу симплекс-методом; б) составить задачу, двойственную данной, и решить ее на компьютере; |
| Объём работы: | ТулГУ Тульский государственный университет, 14 стр. |
| Цена: | 750 руб. |
| Замечания: | 85168, оригинальность 50.00% |
| Методичка: | Скачать |
✔ 19 лет на рынке ✔
✔ Средний балл 4,8 ✔
✔ Все типы заданий ✔
Ангелина Бахтиярова
Заказывала работу на Вашем сайте. В задание нужно было решить кейс-задание и обычные задачи по праву. Всего 9 заданий было. Все ответы были расписаны подробно, даже ссылки на статьи закона были. Задачи приняли с первого раза. Быстро сделали, всего за 2 дня. Спасибо за работу! Буду к Вам обращаться! Надеюсь следующие заказы будут так же быстро и качественно выполняться!’
Источник
Задачи оптимизации
Задача № 1. Решить графическим методом типовую задачу оптимизации.
Некоторая фирма выпускает два набора удобрений для газонов: обычный и улучшенный. В обычный набор входит 3 кг азотных, 4 кг фосфорных и 1 кг калийных удобрений, а в улучшенный – 2 кг азотных, 6 кг фосфорных и 3 кг калийных удобрений. Известно, что для некоторого газона требуется по меньшей мере 10 кг азотных, 20 кг фосфорных и 7 кг калийных удобрений. Обычный набор стоит 3 ден. ед., а улучшенный – 4 ден. ед. Какие и сколько наборов удобрений нужно купить, чтобы обеспечить эффективное питание почвы и минимизировать стоимость?
Построить экономико-математическую модель задачи, дать необходимые комментарии к ее элементам и получить решение графическим методом. Что произойдет, если решать задачу на максимум и почему?
1. Введем переменные:
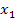
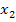
2. Зададим целевую функцию. Задача на минимизацию затрат. Запишем уравнение, описывающее затраты
Найдем решение сформированной задачи, используя ее геометрическую интерпретацию. Сначала определим область допустимых решений. Для этого в неравенствах системы ограничений знаки неравенств заменим на знаки точных равенств, и найдем соответствующие прямые:
Выразим 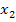
Для построения прямой достаточно двух точек, найдем их координаты:
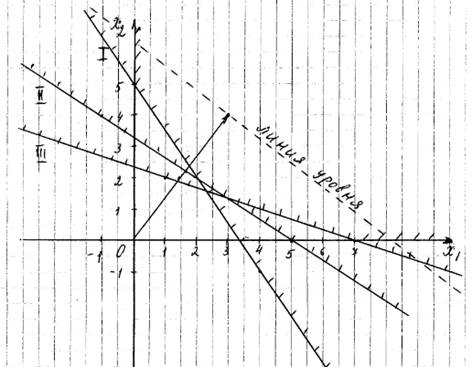
Эти прямые изображены на рисунке 1. Условие неотрицательности показывает, что искомая область располагается в первой четверти.
Каждая из построенных прямых делит плоскость на две полуплоскости. Координаты точек одной полуплоскости удовлетворяют исходному неравенству, а другой – нет. Чтобы определить искомую полуплоскость, нужно взять какую-нибудь точку, принадлежащую одной из полуплоскостей, и проверить, удовлетворяют ли ее координаты данному неравенству. Если координаты взятой точки удовлетворяют данному неравенству, то искомой является та полуплоскость, которой принадлежит эта точка, в противном случае – другая полуплоскость.
Рисунок 1. Графический метод решения
На рисунке 1, область допустимых решений не ограничена и отмечена штрихом. Координаты любой точки, принадлежащей этой области, удовлетворяют данной системе неравенств и условию неотрицательности переменных. Поэтому сформулированная задача будет решена, если мы сможем найти точку, принадлежащую области допустимых решений, в которой целевая функция принимает минимальное значение. Чтобы найти указанную точку, построим вектор 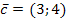
Так как задача на минимум, то линию уровня будем двигать по направлению вектора. Первая точка касания и будет оптимальным решением. Координаты этой точки и определяют оптимальные количества обычных и улучшенных наборов удобрений, при которых затраты являются минимальными.
В данном примере это точка пересечения прямых I и 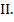
Следовательно, если фирма купит 2 обычных и 2 улучшенных набора удобрений, то минимальные затраты составят
Если данную задачу решать на максимум, то линия уровня будет сдвигаться вправо до бесконечности (так область решений не ограничена). Таким образом, конечного решения не будет.
Задача № 2. Предложить оптимальное управленческое решение в следующих типовых хозяйственных ситуациях.
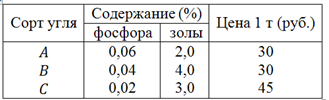
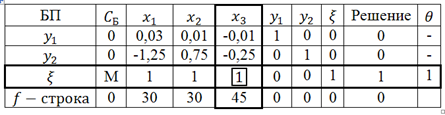
Металлургическому заводу требуется уголь с содержанием фосфора не более 0,03% и с долей зольных примесей не более 3,25%. Завод закупает три сорта угля 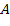
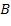
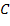
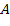
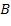
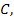
Введем следующие обозначения: 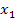
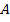
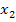
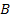
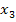
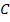
Целевая функция задачи:
Таким образом, ЭММ задачи имеет вид:
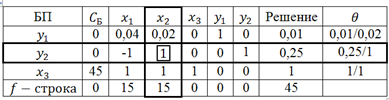
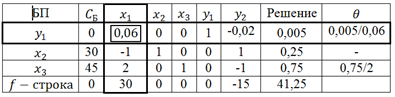
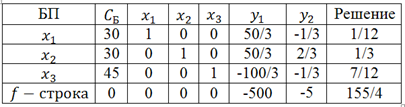
Решим данную задачу симплекс-методом. Преобразуем исходную модель. В ограничения типа 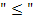
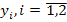
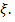
Заполним первую симплекс-таблицу.
В 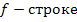
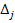
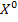
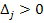
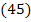
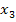
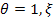
В 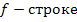
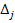
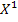
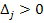
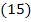
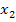
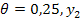
В 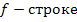
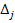
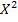
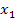
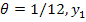
В 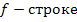
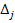
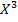
Полученное оптимальное решение означает, что для получения 1 т угля необходимо взять 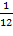
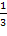
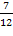
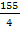
Задача № 3. Провести моделирование и решить специальную задачу линейного программирования.
Компания, занимающаяся ремонтом автомобильных дорог, в следующем месяце будет проводить ремонтные работы на пяти участках автодорог. Песок на участки ремонтных работ может доставляться из трех карьеров, месячные объемы предложений по карьерам известны. Из планов производства ремонтных работ известны месячные объемы потребностей по участкам работ. Имеются экономические оценки транспортных затрат (в у. е.) на перевозку 1тонны песка с карьеров на ремонтные участки.
Числовые данные для решения содержатся ниже в Матрице планирования. Требуется:
1) Предложить план перевозок песка на участки ремонта автодорог, который обеспечивает минимальные совокупные транспортные издержки.
2) Что произойдет с оптимальным планом, если изменятся условия перевозок: а) появится запрет на перевозки от первого карьера до второго участка работ?; б) по этой коммуникации будет ограничен объем перевозок 3 тоннами?
Источник