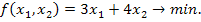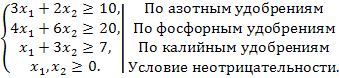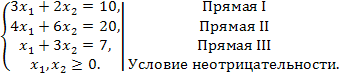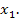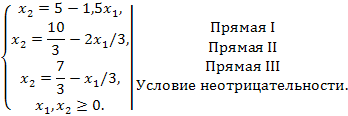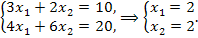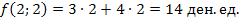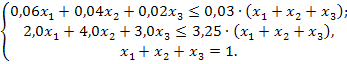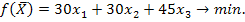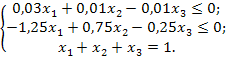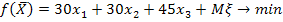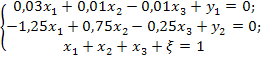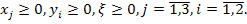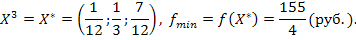Контрольная работа: Экономико-математическое моделирование анализа ресурсов
1. Некоторая фирма выпускает два набора удобрений для газонов: обычный и улучшенный. В обычный набор входит 3 кг азотных, 4 кг фосфорных и 1 кг калийных удобрений, а в улучшенный – 2 кг азотных, 6 кг фосфорных и 3 кг калийных удобрений. Известно, что для некоторого газона требуется по меньшей мере 10 кг азотных, 20 кг фосфорных и 7 кг калийных удобрений. Обычный набор стоит 3 ден. Ед., а улучшенный – 4 ден. Ед. какие и сколько наборов удобрений нужно купить, чтобы обеспечить эффективное питание почвы и минимизировать стоимость?
Построить экономико-математическую модель задачи, дать необходимые комментарии к ее элементам и получить решение графическим методом. Что произойдет, если решать задачу на максимум, и почему?
| стоимость | 3 | 4 | |
| Состав удобрения | Количество удобрений | Необходимый минимум | |
| обычное | улучшенное | ||
| Азотное | 3 | 2 | 10 |
| Фосфорное | 4 | 6 | 20 |
| Калийное | 1 | 3 | 7 |
1 составим математическую модель:
Обозначим через xj количество кг удобрения
x1- количество кг обычного удобрения;
x2- количество кг улучшенного удобрения.
Цель – наименьшая стоимость удобрения,

По азотным удобрениям 3х1+2х2≥10
По фосфорным удобрениям 4х1+6х2≥20
По калийным удобрениям 1х1+3х2≥7
По смыслу х1≥0 х2≥0
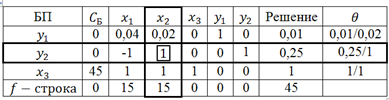
Решим графическим способом.
Первое ограничение (по азоту) имеет вид 3х1+2х2≥10 найдем пересечение с осями координат, т. е. 3х1+2х2=10 – l1
| Х1 | 0 | 10/3 |
| Х2 | 5 | 0 |
0 отчета Устойчивости.
Полученное решение означает, что максимальную выручку 460 ден ед, можем получит при выпуски 80 ед продукции А и 10 ед продукции Г. При это ресурсы 2 и 3 типа будут использоваться полностью, а из 200 ед сырья 1 типа будет использоваться 180 ед сырья.
Сформулируем экономико–математическую модель двойственной задачи
у1- двойственная оценка ресурса 1 типа, или цена 1 ресурса,
у2- двойственная оценка ресурса 2 типа, или цена 2 ресурса,
у3- двойственная оценка ресурса 3 типа, или цена 3 ресурса.
Целевая функция двойственной задачи: необходимо найти такие «цены» у на ресурсы, чтобы общая стоимость используемых ресурсов была минимальной. G=b1*y1+b2*y2+…→min
Вы исходной задачи четыре переменных, следовательно в двойственной задаче четыре ограничения.


по виду продукции Б: у1+2у2+4у3≥7,
по виду продукции В: 3у1+4у2+у3≥3,
по виду продукции Г: 2у1+8у2+у3≥6
по смыслу у1; у2; у3≥0
Найдем оптимальный план двойственной задачи, используя теоремы двойственности:
По 2 теореме- yi*(∑aij*xj-bi)=0 и xj(∑aij*yi-cj)=0,
у1*(2х1+х2+3х3+2х4-200)=0 → у1(2*80+0+3*0+2*10-200)=0 180 0 и х4=10>0, поэтому первое и четвертое ограничение двойственной задачи обращаются в равенство:


Выразим через у2=5-2у3,
у1=0; у2=7/15; у3=34/15
Проверим выполняемость первой теоремы двойственности:
В нашей задачи в план выпуска не вошла продукция Б и В, потому что затраты по ним превышают цену на 3 ден ед (10-7=3) и 1,133 ден ед (4,1333-3=1,133) соответственно.
Подставим в ограничения двойственной задачи оптимальные значения у:
Так как запас ресурсов 1, 2 типа сырья изменяться на 8 и 10 единицы (увеличиться) и 3 типа уменьшаться на 5 единиц. Из теоремы об оценках известно, что колебание величины bi приводит к увеличению или уменьшению F.
F=8*0+10*7/15+(-5)*34/15=-6,667, следовательно, увеличение запасов ресурсов 1 и 2 типа на 8 и 10 ед. и уменьшение 3 типа на 5 ед приведет к уменьшению значения целевой функции на -6,667 ден ед.
По условию задачи для изготовления изделия Д используется:
Сырье 1 типа а*1=2,
Сырье 2 типа а*2=2,
Сырье 3 типа а*3=2
Ожидаемая прибыль от данного изделия Д с*=10 ден ед.
Для оценки целесообразности продукта Д, рассчитаем чистый доход
следовательно, целесообразно включать в план изделие Д, т.к. е=4,533>0.
3. Промышленная группа предприятий (холдинг) выпускает продукцию трех видов, при этом каждое из трех предприятий группы специализируется на выпуске продукции одного вида: первое предприятие специализируется на выпуске продукции одного вида: первое предприятие специализируется на выпуске продукции первого вида, второе предприятие – продукции второго вида, третье предприятие – продукции третьего вида. Часть выпускаемой продукции потребляется предприятиями холдинга (идет на внутреннее потребление) остальная часть поставляется за его пределы (внешним потребителями, является конечным продуктом). Специалистами управляющей компании получены экономические оценки aij(i=1,2,3; j=1,2,3) элементов технологической матрицы А (норм расхода, коэффициентов прямых материальных затрат) и элементов уi вектора конечной продукции У.
Проверить продуктивность технологической матрицы А=(аij) (матрицы коэффициентов прямых материальных затрат).
Построить баланс (заполнить таблицу) производства и распределения продукции предприятий холдинга.
| предприятия | коэффициенты прямых затрат | конечный продукт | ||
| 1 | 2 | 3 | ||
| 1 | 0,2 | 0,1 | 0,2 | 150 |
| 2 | 0 | 0,1 | 0,2 | 180 |
| 3 | 0,1 | 0 | 0,1 | 100 |
Найдем продуктивность А с помощью достаточного условия ||A||max(0,3;0,2;0,5)=0,5 ркр=2 следовательно, свойство случайности выполняется.
Для проверки независимости уровней ряда остатков:
1 вычислим d- статистику (критерий Дарбина – Уотсона)
2 вычислить первый коэффициент автокорреляции r(1)
для расчетов подготовим –
∑e2(t) = 14,6 — используем Excel fx/математическая/СУММКВ),
∑(e(t)-e(t-1))2 = 32,32 – используем Excel fx/математическая/СУММКВРАЗН) – 1 массив кроме 1-го, 2 массив кроме последнего.
d=∑(e(t)-e(t-1))2 / ∑e2(t) = 32,32/14,6=2,213699
По таблице Значения d-критерия Дарбина – Уотсона определим, что d1= 1,08 и d2= 1,36
Т.е. наше d=2,213699 € (1.08;1,36), следовательно нужна дополнительная проверка, найдем d’=4-d=4-2,213699=1,786301, т.е d’ € (1,36;2)


следовательно, свойство независимости уровней ряда остатков выполняются, остатки независимы.
Для проверки нормального распределения остатков вычислим R/S – статистику
еmax- максимальный уровень ряда остатков,
еmin- минимальный уровень ряда остатков,
S- среднеквадратичное отклонение.
еmax=2,2333333 используем Excel fx/статистическая/МАКС),
еmin=-2,466666667 используем Excel fx/статистическая/МИН),
Se=1,444200224 1-я таблица Итогов регрессии строка «стандартная ошибка»
Следовательно, R/S=2,2333333 — (-2,466666667)/ 1,444200224=3,254396
Критический интервал (2,7;3,7), т.е R/S=3,254396 € (2,7;3,7), свойство нормального распределения остатков выполняется.
Подводя итоги проверки можно сделать вывод, что модель ведет себя адекватно.
Для оценки точности модели вычислим среднюю относительную ошибку аппроксимации Еотн = |e(t)/Y(t)|*100% по полученным значениям определить среднее значение (fx/математическая/СРЗНАЧ)
| относит. погр-ти |
| 28,88888889 |
| 6,19047619 |
| 7,333333333 |
| 8,787878788 |
| 2,222222222 |
| 2,156862745 |
| 4,444444444 |
| 8,933333333 |
| 10,72463768 |
Eотн ср =8,853564 – хороший уровень точности модели
Для вычисления точечного прогноза в построенную модель подставим соответствующие значения t=10 и t=11:
Ожидаемый спрос на кредитные ресурсы финансовой компании на 10 неделю должен составить около 28,16666667 млн. руб., а на 11 неделю около 30,86666667 млн. руб.
При уровне значимости L=30%, доверительная вероятность равна 70%, а критерий Стьюдента при к=n-2=9-2=7, равен
Se=1,444200224 1-я таблица Итогов регрессии строка «стандартная ошибка»,
t’ср = 5(fx/математическая/СРЗНАЧ) — средний уровень по рассматриваемому моменту времени,
Ширину доверительного интервала вычислим по формуле:
Далее вычислим верхнюю и нижнюю границы прогноза uниж=y10-u1; uверх=у10+u1; uниж=y11-u1; uверх=у10+u1
Спрос на кредитные ресурсы финансовой компании на 10 неделю в пределах от 26,16888 млн. руб. до 30,16445 млн. руб., а на 11 неделю от 28,75241 млн. руб. до 32,98093 млн. руб.
Источник
Задачи оптимизации
Задача № 1. Решить графическим методом типовую задачу оптимизации.
Некоторая фирма выпускает два набора удобрений для газонов: обычный и улучшенный. В обычный набор входит 3 кг азотных, 4 кг фосфорных и 1 кг калийных удобрений, а в улучшенный – 2 кг азотных, 6 кг фосфорных и 3 кг калийных удобрений. Известно, что для некоторого газона требуется по меньшей мере 10 кг азотных, 20 кг фосфорных и 7 кг калийных удобрений. Обычный набор стоит 3 ден. ед., а улучшенный – 4 ден. ед. Какие и сколько наборов удобрений нужно купить, чтобы обеспечить эффективное питание почвы и минимизировать стоимость?
Построить экономико-математическую модель задачи, дать необходимые комментарии к ее элементам и получить решение графическим методом. Что произойдет, если решать задачу на максимум и почему?
1. Введем переменные:
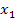
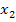
2. Зададим целевую функцию. Задача на минимизацию затрат. Запишем уравнение, описывающее затраты
Найдем решение сформированной задачи, используя ее геометрическую интерпретацию. Сначала определим область допустимых решений. Для этого в неравенствах системы ограничений знаки неравенств заменим на знаки точных равенств, и найдем соответствующие прямые:
Выразим 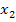
Для построения прямой достаточно двух точек, найдем их координаты:
Эти прямые изображены на рисунке 1. Условие неотрицательности показывает, что искомая область располагается в первой четверти.
Каждая из построенных прямых делит плоскость на две полуплоскости. Координаты точек одной полуплоскости удовлетворяют исходному неравенству, а другой – нет. Чтобы определить искомую полуплоскость, нужно взять какую-нибудь точку, принадлежащую одной из полуплоскостей, и проверить, удовлетворяют ли ее координаты данному неравенству. Если координаты взятой точки удовлетворяют данному неравенству, то искомой является та полуплоскость, которой принадлежит эта точка, в противном случае – другая полуплоскость.
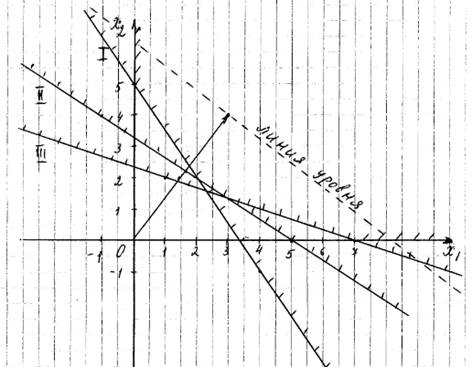
Рисунок 1. Графический метод решения
На рисунке 1, область допустимых решений не ограничена и отмечена штрихом. Координаты любой точки, принадлежащей этой области, удовлетворяют данной системе неравенств и условию неотрицательности переменных. Поэтому сформулированная задача будет решена, если мы сможем найти точку, принадлежащую области допустимых решений, в которой целевая функция принимает минимальное значение. Чтобы найти указанную точку, построим вектор 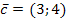
Так как задача на минимум, то линию уровня будем двигать по направлению вектора. Первая точка касания и будет оптимальным решением. Координаты этой точки и определяют оптимальные количества обычных и улучшенных наборов удобрений, при которых затраты являются минимальными.
В данном примере это точка пересечения прямых I и 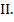
Следовательно, если фирма купит 2 обычных и 2 улучшенных набора удобрений, то минимальные затраты составят
Если данную задачу решать на максимум, то линия уровня будет сдвигаться вправо до бесконечности (так область решений не ограничена). Таким образом, конечного решения не будет.
Задача № 2. Предложить оптимальное управленческое решение в следующих типовых хозяйственных ситуациях.
Металлургическому заводу требуется уголь с содержанием фосфора не более 0,03% и с долей зольных примесей не более 3,25%. Завод закупает три сорта угля 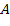
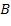
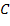
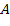
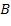
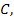
Введем следующие обозначения: 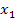
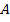
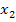
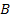
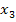
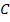
Целевая функция задачи:
Таким образом, ЭММ задачи имеет вид:
Решим данную задачу симплекс-методом. Преобразуем исходную модель. В ограничения типа 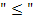
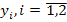
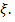
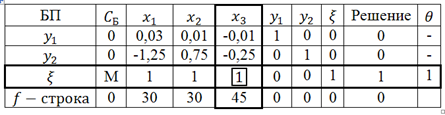
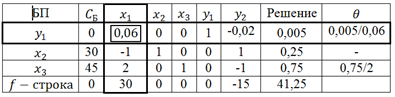
Заполним первую симплекс-таблицу.
В 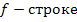
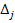
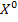
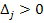
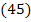
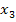
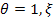
В 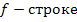
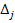
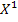
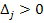
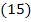
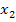
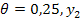
В 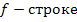
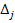
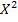
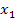
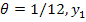
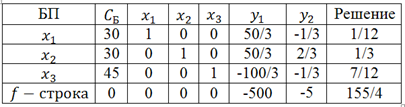
В 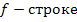
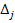
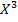
Полученное оптимальное решение означает, что для получения 1 т угля необходимо взять 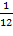
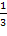
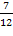
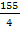
Задача № 3. Провести моделирование и решить специальную задачу линейного программирования.
Компания, занимающаяся ремонтом автомобильных дорог, в следующем месяце будет проводить ремонтные работы на пяти участках автодорог. Песок на участки ремонтных работ может доставляться из трех карьеров, месячные объемы предложений по карьерам известны. Из планов производства ремонтных работ известны месячные объемы потребностей по участкам работ. Имеются экономические оценки транспортных затрат (в у. е.) на перевозку 1тонны песка с карьеров на ремонтные участки.
Числовые данные для решения содержатся ниже в Матрице планирования. Требуется:
1) Предложить план перевозок песка на участки ремонта автодорог, который обеспечивает минимальные совокупные транспортные издержки.
2) Что произойдет с оптимальным планом, если изменятся условия перевозок: а) появится запрет на перевозки от первого карьера до второго участка работ?; б) по этой коммуникации будет ограничен объем перевозок 3 тоннами?
Источник
detector