Ответы к страницам 249-250 №1033-1047 ГДЗ к учебнику Математика 5 класс Мерзляк, Полонский, Якир
Параграф 36. Среднее арифметическое
Задание № 1033
Найдите среднее арифметическое чисел:
1) 10,3 и 9,1;
2) 2,8; 16,9 и 22.
(10,3 + 9,1) : 2 = 19,4 : 2 = 9,7
(2,8 + 16,9 + 22) : 3 = 41,7 : 3 = 13,9
Задание № 1034
Найдите среднее арифметическое чисел:
1) 4,2 и 2,1;
2) 3,9; 6; 9,18 и 15,8.
(4,2 + 2,1) : 2 = 6,3 : 2 = 3,15
(3,9 + 6 + 9,18 + 15,8) : 4 = 34,88 : 4 = 8,72
Задание № 1035
В течении недели в 8 ч утра Саша измерял температуру воздуха. Он получил такие результаты: 20°С; 18°С; 16°С; 15°С; 14°С; 17°С; 19°С. Найдите среднее значение проведенных измерений.
(20 + 18 + 16 + 15 + 14 + 17 + 19) : 7 = 119 : 7 = 17
Ответ: 17°С.
Задание № 1036
Найдите среднюю оценку учеников вашего класса по математике за II четверть. Ответ округлите до единиц.
Нужно сложить оценки по математике за II четверть всех учеников вашего класса и полученную сумму поделить на количество учеников в вашем классом.
Задание № 1037
1) Поезд ехал со скоростью 4 ч со скоростью 64 км/ч и 5 ч со скоростью 53,2 км/ч. Найдите среднюю скорость поезда на протяжении всего пути.
1) 64 * 4 = 256 (км) — проехал поезд за первые 4 часа пути.
2) 53,2 * 5 = 266 (км) — проехал поезд за вторые 5 часов пути.
3) ) 256 + 266 = 522 (км) — длина всего пути.
4) 4 + 5 = 9 (ч) — поезд был в пути.
5) 522 : 9 = 58 (км/ч) — средняя скорость поезда на протяжении всего пути.
Ответ: 58 км/ч.
2) В автомастерской работает 10 человек. У двоих из них месячная зарплата составляет 22800 р., у четверых — 28000 р., у троих 31000 р., а у одного 32000 р. Какова средняя зарплата работников мастерской?
1) 2*22800 + 4*28000 + 3*31000 + 32000 = 282600 (р.) — получают все работники
2) 282600 : 10 = 28260 (р.) — средняя зарплата работников мастерской
Ответ: 28260 р.
Задание № 1038
1) Автомобиль ехал 3 ч со скоростью 56,4 км/ч и 4 ч со скоростью 62,7 км/ч. Найдите среднюю скорость автомобиля на всем пути.
1) 56,4 * 3 = 169,2 (км) — проехал автомобиль за первые 3 часа пути.
2) 62,7 * 4 = 250,8 (км) — проехал автомобиль за вторые 4 часа пути.
3) 169,2 + 250,8 = 420 (км) — длина всего пути.
4) 3 + 4 = 7 (ч) — ехал автомобиль весь путь.
5) 420 : 7 = 60 (км/ч) — средняя скорость автомобиля на всем пути.
Ответ: 60 км/ч.
2) Фермер собрал с каждого гектара поля площадью 30 га по 30,2 ц пшеницы, а с каждого гектара поля площадью 20 га — по 32, 3 ц пшеницы. Какой средний урожай с одного гектара собрал фермер.
1) 30,2 * 30 = 906 (ц) — пшеницы собрал фермер с первого поля
2) 32,3 * 20 = 646 (ц) — пшеницы собрал фермер со второго поля
3) 906 + 646 = 1552 (ц) — пшеницы собрал фермер с обеих полей
4) 30 + 20 = 50 (га) — площадь двух полей
5) 1552 : 50 = 31,04 (ц) — средний урожай с одного гектара
Ответ: 31,04 ц пшеницы.
Задание № 1039
Среднее арифметическое чисел 7,8 и x равно 7,2. Найдите число x.
Задание № 1040
Среднее арифметическое чисел 6,4 и y равно 8,5. Найдите число y.
Задание № 1041
Среднее арифметическое двух чисел, одно из которых в 4 раза меньше второго, равно 10. Найдите эти числа.
Решение задачи через х
Пусть x − одно число, тогда:
4x − второе число.
Составим уравнение:
(x + 4x) : 2 = 10
5x = 10 * 2
x = 20 : 5
x = 4 − одно число;
4x = 4 * 4 = 16 − второе число.
Ответ: 4 и 16.
Задание № 1042
Среднее арифметическое двух чисел, одно из которых на 4,6 больше второго, равно 8,2. Найдите эти числа.
Пусть x − второе число, тогда:
x + 4,6 − первое число.
Составим уравнение:
(x + x + 4,6) : 2 = 8,2
2x + 4,6 = 8,2 * 2
2x = 16,4 − 4,6
x = 11,8 : 2
x = 5,9 − второе число;
x + 4,6 = 5,9 + 4,6 = 10,5 − первое число.
Ответ: 5,9 и 10,5.
Задание № 1043
Отметьте на координатном луче числа а и b и их среднее арифметическое, если: 1) а = 2, b = 6; 2) а = 4, b = 7. Как расположена точка, соответствующая среднему арифметическому чисел а и b, относительно точек, соответствующих числам а и b?
а b
.____.____.____.__
0 2 4 6
Точка расположена точно посередине отрезка ab на одинаковом расстоянии от этих точек.
Задание № 1044
Принимая участие в математической олимпиаде, Дима решил 10 задач. За каждую задачу он мог получить не более 12 баллов. За первые восемь задач мальчик получил среднюю оценку 7 баллов. Сколько баллов получил Дима за каждую из оставшихся двух задач, если среднее количество баллов за одну задачу составляло 8 баллов?
1) 7 * 8 = 56 (б.) — набрал Дима за первые восемь задач.
2) 8 * 10 = 80 (б.) — набрал Дима за все 10 задач.
3) 80 − 56 = 24 (б.) — набрал Дима за последние две задачи.
4) 24 : 2 = 12 (б.) — набрал Дима за каждую из оставшихся двух задач.
Ответ: по 12 баллов.
Задание № 1045
Автомобиль ехал 3,4 ч по шоссе со скоростью 90 км/ч и 1,6 ч по грунтовой дороге. С какой скоростью ехал автомобиль по грунтовой дороге, если средняя скорость на протяжении всего пути составляла 75,6 км/ч?
1) 90 * 3,4 = 306 (км) — проехал автомобиль по шоссе.
2) 3,4 + 1,6 = 5 (ч) — общее время в пути.
3) 75,6 * 5 = 378 (км) — длина всего пути.
4) 378 − 306 = 72 (км) — проехал автомобиль по грунтовой дороге.
5) 72 : 1,6 = 45 (км/ч) — скорость автомобиля по грунтовой дороге.
Ответ: 45 км/ч.
Задание № 1046?
Купили 2 кг конфет одного вида по 255 р. за килограмм, 4 кг конфет второго вида по 285 р. за килограмм и еще 3 кг конфет третьего вида. Средняя цена купленных конфет составляла 260 р. за килограмм. Сколько стоил килограмм конфет третьего вида?
1) 255 * 2 = 510 (р.) — потратили на конфеты первого вида.
2) 285 * 4 = 1140 (р.) — потратили на конфеты второго вида.
3) 510 + 1140 = 1650 (р.) — потратили за конфеты первых двух видов.
4) 2 + 4 + 3 = 9 (кг) — конфет купили всего.
5) 260 * 9 = 2340 (р.) — потратили на конфеты всего.
6) 2340 − 1650 = 690 (р.) — потратили на конфеты третьего вида.
7) 690 : 3 = 230 (р.) — стоил килограмм конфет третьего вида.
Ответ: 230 рублей.
Задание № 1047
Среднее арифметическое четырех чисел равно 2,1, а среднее арифметическое трех других чисел − 2,8. Найдите среднее арифметическое этих семи чисел.
1) 2,1 * 4 = 8,4 — сумма четырех чисел.
2) 2,8 * 3 = 8,4 — сумма трех чисел.
3) 8,4 + 8,4 = 16,8 — сумма всех семи чисел.
4) 16,8 : 7 = 2,4 — среднее арифметическое этих семи чисел.
Ответ: 2,4.
Источник
Какой урожай пшеницы можно собирать с 1 гектара
Прибыль от выращивания зерновых является ключевым аспектом в аграрном бизнесе. Для получения отличных результатов и повышения плодородности нужно приложить немало усилий.
Количество зерна, которое можно собрать с 1 га земли, является основным показателем урожайности пшеницы. На этот показатель влияет множество факторов – от выбора подходящего сорта и своевременного посева, до процесса сбора урожая.
При соблюдении всех правил и требований для выращивания пшеницы с 1 га можно собрать 50-90 центнера зерна – это очень хороший результат. 30-40 центнер – средний показатель, 10 – очень низкий.
Сорт — основа урожайности
Одним из важнейших этапов является выбор сорта зерновой культуры. Разные сорта имеют разные показатели урожайности и переносимости погодных условий. Учитывая климатические особенности в наших регионах, популярностью пользуются такие сорта пшеницы:
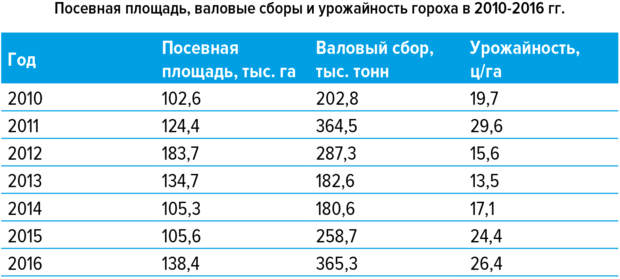
- Московская 56 – в среднем урожайность 75 центнеров с гектара.
- Августа – приблизительно 86 центнеров с гектара.
- Губернатор Дона – 45 центнеров с 1 гектара.
- Галина – 70 центнеров с гектара.
- Немчиновская 56 – примерно 60-70 центнеров с гектара.
Климат и плодородность почвы
Несмотря на достижения в селекции и хорошие показатели данных сортов, нельзя пренебрегать влиянием погодных явлений на то, сколько зерна будет собрано. Прежде всего, имеет значение:
- Влажность воздуха и почвы.
- Сильные морозы и отсутствие снежного покрова.
- Количество и длительность солнечных дней.
В областях с засушливым климатом, при высоком дефиците осадков, даже сорта с потенциально высокой урожайностью 60-70 т/га, могут реализоваться лишь на 15-25%. Суточное потребление воды озимой пшеницы варьируется в зависимости от периода ее роста. На начальных этапах оно составляет всего 17 м3/га, но увеличивается во время фазы кущения. Поэтому, чтобы компенсировать дефицит влаги, целесообразно проводить орошение на начальном этапе в объеме 1000-1400 м3/га и 2-3 полива общим объемом 2800-3200 во время вегетационного периода.
Еще один эффективный способ противодействия неблагоприятному климату – насаждение лесополос.
Они значительно уменьшают скорость ветра на прилегающей площади, что приводит в повышению температуры и влажности воздуха.
В качестве почвы для засева зерновых, предпочтительнее всего использовать черноземы. Недостаток полезных веществ в них легко исправить использованием удобрений. Пшеница благоприятно отзывается на внесение фосфорных и калийных удобрений увеличением урожая, который удается собрать с 1га, что можно проследить по приведенной ниже таблице.
| Навоз т/га | N/P/K | ||
| 0 | 90/60/60 | 180/12/120 | |
| 0 | 35.2 | 41.4 | 48.6 |
| 80 | 44.0 | 49.3 | 52.7 |
Время посева
Сроки посева играют очень важную роль в развитии полноценного колоса в дальнейшем. Проведя множество исследований, аграрии сошлись во мнении, что ранние сроки посева увеличивают шансы на получение хорошего урожая озимой пшеницы.
Засев в конце сентября, или в начале октября позволяет лучше сформироваться корневой системе, повышая урожайность до 20% в сравнении с более поздними сроками.
Полезные предшественники
Немаловажную роль в выращивании пшеницы играют растения предшественники. Прежде всего, они обеспечивают повышение влажности, а значит и сопротивляемость засухам. Поэтому, в засушливых областях, зерновые специально сеют в такой грунт. Лучшими, для возделывания пшеницы, считаются почвы после выращивания бобовых, картофеля, свеклы, пропашных культур. Землю, после уборки предшественников, дискуют.
Особенности сбора урожая
Сбор урожая – один из самых волнующих, важных и ответственных моментов. Началу уборочных работ следует уделять особое внимание. Определяя срок уборки, учитывают сортовые особенности использованного посевного материала. Уборку начинают в период полного созревания зерен и когда их влажность ниже 20%.
Немало зависит и от использования сельскохозяйственной техники. В наших широтах, в основном, применяют метод прямого комбайнирования, что позволяет снизить потери урожая в условиях плохой погоды. Чаще всего используют такие комбайны как Нива, Дон 1500. Выполнив все требования и надеясь на благоприятные погодные условия, можно получить желаемую урожайность около 50 — 90 с 1 га.
Источник
С поля площадью 20 га был собран урожай пшеницы
Получите 30₽ за публикацию своей разработки в библиотеке «Инфоурок»
и получить бесплатное свидетельство о размещении материала на сайте infourok.ru
Попробуйте УМНЫЙ ПОИСК по курсам повышения квалификации и профессиональной переподготовки
Войти с помощью:
КРИВАЯ ПРОИЗВОДСТВЕННЫХ ВОЗМОЖНОСТЕЙ
Кривая (граница) производственных возможностей иллюстрирует проблему выбора в условиях ограниченных ресурсов.
КПВ показывает максимально возможное производство одного продукта при фиксированном выпуске другого продукта и при полном и наилучшем использовании фиксированных ресурсов.
Закон возрастающих альтернативных затрат:
При полном и наилучшем использовании ресурсов по мере увеличения производства одного продукта для получения каждой следующей (дополнительной) его единицы приходится отказываться от другого продукта во всё большем количестве.
КПВ представляет собой выпуклую функцию.
КПВ не является неподвижной. С ростом НТП или доступных ресурсов она сдвигается вправо и вверх, при уменьшении ресурсов граница производственных возможностей смещается влево и вниз.
РЕШЕНИЕ ЗАДАЧ
Задача 1.
На одном однородном поле фермер может произвести 300 тонн картофеля или 100 тонн пшеницы, а на другом – везде альтернативная стоимость выращивания 1 тонны пшеницы равна 2 тоннам картофеля при максимальном производстве картофеля, равном 400 т.
а) Какова альтернативная стоимость производства 1 т пшеницы на первом поле?
б) Построить кривую производственных возможностей для каждого поля.
в) Построить общую КПВ фермера.
Решение.
а) На первом поле, пожертвовав 1 тонной пшеницы, фермер высвободил площадь для выращивания 3 тонн картофеля. Следовательно, альтернативная стоимость производства 1 тонны пшеницы на первом поле равна 3 т картофеля. И, наоборот, 1 т картофеля стоит 1/3 т пшеницы.
б) На первом поле фермер может вырастить максимум 300 тонн картофеля, при этом он должен отказаться выращиванием пшеницы совсем (на графике эта ситуация будет соответствовать точке (300; 0)), или вырастить 100 тонн пшеницы, пожертвовав при этом выращиванием картофеля (получаем соответственно точку (0; 100). Отметим в плоскости эти две точки. Кривой производственных возможностей будет отрезок прямой, соединяющий точки максимального производства пшеницы и наибольшего производства картофеля.
Альтернативная стоимость 1 т пшеницы на втором поле равна 2 т картофеля. При этом максимальное производство картофеля составляет 400 т. Значит, наибольшее количество пшеницы, которое можно вырастить на втором поле, равно 400 : 2 = 200 т. Тогда в координатной плоскости нужно построить точки (0; 400) и (200; 0). КПВ представляет собой отрезок прямой, соединяющей эти точки.
в) На двух полях максимум производства картофеля равен 300 + 400 = 700 (т), а наибольшее количество пшеницы, которое можно вырастить – соответственно равно 100 + 200 = 300 (т). Тогда кривой производственных возможностей будет отрезок прямой с концами в точках (700; 0) и (0; 300). Отметим эти точки на графике.
Далее можно предложить два варианта использования производственных ресурсов: в первом случае график проходит через точку (300; 200) – максимально возможный урожай картофеля на первом поле и максимально возможный урожай пшеницы на втором поле; во втором случае – через точку (400; 100) – максимально возможный урожай картофеля на втором поле и максимально возможный урожай пшеницы на первом поле.
Ясно, что верное решение даёт первый вариант, так как в первом случае получается выпуклая кривая, а во втором – вогнутая.
Допустим, что мы всегда засевали все поля пшеницей, а на следующий год нам потребовалось немного картофеля. На каком поле его посадить? Ясно, что на том, где потери в виде недополученной пшеницы будут минимальными, т.е. там, где альтернативная стоимость картофеля наименьшая.
В данном случае следует посадить картофель на первом поле. Если не хватит этого поля, то остаток картофеля надо посадить на поле со следующим по возрастанию значением альтернативной стоимости картофеля и т.д.
Ответ: а) 3 т; б) и в) на рисунках.
Задача 2.
Королевство «Рубляндия» может производить два знаменитых продукта: «масло» и «пушки» (образы мирной и военной продукции) и имеет следующую границу годовых производственных возможностей:
Эту кривую можно представить в табличном виде по точкам перелома:
а) Каково максимально возможное производство пушек?
Ответ: 8 тыс. штук при отсутствии производства масла.
б) Сколько может быть произведено пушек при производстве 7 тыс. тонн масла?
Ответ: не более 6 тыс. пушек.
в) Найти альтернативную стоимость увеличения производства пушек с 6 тыс. до 7 тыс. в год.
Решение.
М (6) = 7 тыс. тонн/год,
М (7) = 4 тыс. тонн/год.
Альтернативная стоимость увеличения производства пушек будет равна:
М (6) – М (7) = 7 – 4 = 3 (тыс. тонн/год)
г) На сколько может быть увеличен выпуск масла при производстве 4 тыс. тонн масла и 4 тыс. штук пушек?
Решение.
М (4) = 10 тыс. тонн/год,
М (7) = 4 тыс. тонн/год.
Выпуск масла может быть увеличен с 4 тыс. тонн до 10 тыс. тонн, т.е. на
10 – 4 = 6 (тыс. тонн/год).
д) Можно ли произвести с помощью имеющихся ресурсов 6,7 тыс пушек и 5,5 тыс. тонн масла?
Решение.
Нет, нельзя, поскольку выпуск 5,5 тыс. тонн масла на КПВ соответствует производству 6,5 тыс. пушек.
е) Какова максимальная альтернативная стоимость производства 1 тысячи пушек?
Решение.
М (7) – М (8) = 4 – 0 = 4 тыс. тонн масла.
Ответ: 4 тыс. тонн масла.
ж) Ведущие специалисты Рубляндии оценивают ценность 1 тыс. пушек в 1 млрд. дукатов, а 1 тысячи тонн масла – в 1,5 млрд. дукатов. Сколько нужно произвести пушек и масла, чтобы их общая ценность была наибольшей?
Решение.
Максимум достигается либо в крайних точках графика, либо в точках переломов (в математике говорим: на концах промежутка или в критических точках, в нулях производной функции).
Перебирая все возможные варианты, получим:
F (0; 12) = 0 ∙ 1 + 12 ∙ 1,5 = 18 (млрд. дукатов),
F (4; 10) = 4 ∙ 1 + 10 ∙ 1,5 = 19 (млрд. дукатов),
F (6; 7) = 6 ∙ 1 + 7 ∙ 1,5 = 16,5 (млрд. дукатов),
F (7; 4) = 7 ∙ 1 + 4 ∙ 1,5 = 13 (млрд. дукатов),
F (8; 0) = 8 ∙ 1 + 0 ∙ 1,5 = 8 (млрд. дукатов).
Ответ: 19 млрд. дукатов.
Задача 3.
Могут ли следующие точки лежать на одной кривой производственных возможностей:
А (15; 3), В (8; 13), С (13; 6), D (5; 12)?
Решение.
Если точки принадлежат некоторой КПВ, то соединив эти точки, мы получим некоторую выпуклую кривую. В данном случае, соединив указанные точки, мы имеем кривую, которая не является выпуклой (нет роста вправо-вверх).
Другое решение.
Заметим, что из точки D в точку В можно попасть, только увеличив сразу две координаты. Но для КПВ характерно то, что при увеличении одной координаты мы должны получить уменьшение другой координаты.
Общий алгоритм решения.
Расположить все точки по возрастанию одной из координат. Тогда, если они могут лежать на одной КПВ, то числа по другой координате будут убывать в соответствии с законом возрастающих альтернативных затрат. Если же этого нет, то данные точки не могут принадлежать никакой КПВ.
Ответ: нет.
Задача 4.
Допустим, точки А (4000; 11000), В (8000; 3000), С (7000; Х), D (3000; Y) лежат на одной КПВ. Определить полный набор соотношений с участием Х и Y.
Решение.
Построим данные точки в координатной плоскости ОХY.
По рисунку видно, что для обеспечения выпуклости возможной КПВ необходимо, чтобы 3000 k4.
Ответ: нет, т.к. не выполняется закон возрастающих альтернативных затрат (видно на графике).
Задача 8.
Средневековый кузнец специализируется на копьях и плугах. Могут ли его альтернативные производственные возможности описываться следующими данными?
Решение.
Решается так же, как и задача 7.
Ответ: нет, т.к. не выполняется закон возрастающих альтернативных затрат (видно на графике).
Задача 9.
На одном поле фермер может произвести 500 тонн картофеля или 100 тонн пшеницы, а на другом альтернативная стоимость выращивания 2 тонн пшеницы равна 5 т. картофеля при максимальном производстве картофеля, равном 1000 тонн. Построить кривую производственных возможностей фермера.
Решение.
КПВ представлена на рисунке ниже.
Задача 10.
Фермер имеет три поля, каждое из которых однородно, хотя их продуктивность неодинакова. Поля используются под картофель и пшеницу. На первом поле фермер может вырастить либо 16 тонн картофеля, либо 4 тонны пшеницы, на втором – 8 тонн и 3 тонны соответственно, на третьем – 4 тонны и 2 тонны. Построить кривую производственных возможностей фермера.
Решение.
КПВ представлена на рисунке ниже.
Задача 11.
Фирма изготавливает два типа футбольных мячей, тратя на их производство по 2 часа на каждый мяч. Нарисуйте КПВ фирмы при годовом фонде рабочего времени 7200 часов и выведите её уравнение.
Решение.
КПВ представлена на рисунке ниже.
Задача 12.
Фермер владеет тремя полями площадью 100, 150 и 200 га, урожайность которых оценивается в 25, 20 и 15 центнеров пшеницы с гектара и в 50, 60 и 60 центнеров кукурузы с гектара соответственно. Постройте КПВ и задайте её таблично.
Решение.
КПВ представлена на рисунке ниже.
Заполним таблицу точек перелома графика КПВ:
Задача 13.
Два фермера – Пётр и Павел – могут выращивать свеклу и картофель, засевая ими свои угодья в любой пропорции. Если Пётр все свои поля площадью 100 га отведёт под свеклу, то соберёт урожай 3000 тонн, а если под картофель, то получит 2000 тонн. У Павла земли больше – 150 га, но она похуже, и он может получить 4800 тонн свеклы и 2400 тонн картофеля. Определить точки перелома кривой производственных возможностей совместного труда фермеров, за исключением крайних точек.
Решение.
КПВ представлена на рисунке ниже.
Ответ: (4800; 2000).
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Задача 14.
Фермер имеет три поля, каждое из которых однородно, хотя их продуктивность неодинакова. Поля используются под картофель и пшеницу. На первом поле фермер может вырастить либо 160 тонн картофеля, либо 50 тонн пшеницы, на втором – 300 тонн и 100 тонн соответственно, на третьем – 140 тонн и 60 тонн. Определить точки перелома кривой производственных возможностей совместного труда фермеров, за исключением крайних точек.
Ответ: (160; 160), (460; 60).
Задача 15.
Используя наилучшим образом два своих поля, фермер имеет следующую КПВ (см. рисунок под текстом задачи).
Найдите верные утверждения среди следующих:
а) Альтернативной стоимостью производства первых 600 тонн пшеницы является производство 600 тонн картофеля.
б) Альтернативной стоимостью производства последних 300 тонн картофеля является производство 300 тонн пшеницы.
в) При производстве картофеля в размере 250 тонн альтернативной стоимостью 1 тонны пшеницы будут 3 тонны картофеля.
г) КПВ показывает максимально возможное производство картофеля при заданном уровне производства пшеницы.
д) Нельзя произвести 500 тонн пшеницы и 700 тонн картофеля.
е) При производстве 300 тонн пшеницы альтернативной стоимостью 1 тонны картофеля будет 1 тонна пшеницы.
ж) Для увеличения производства пшеницы с 500 тонн до 700 тонн нужно пожертвовать снижением урожая картофеля на 400 тонн.
Ответ: а, б, в, г, е, ж.
Задача 16.
Ниже приведена КПВ фермера, который выращивает пшеницу и картофель на двух полях.
а) Какова альтернативная стоимость производства 1 тонны картофеля, если его выращивается 75 тонн? 150 тонн? Какова при этом альтернативная стоимость 1 тонны пшеницы?
б) Определить альтернативную стоимость выращивания первых 50 тонн пшеницы?
в) Вычислить среднюю урожайность пшеницы и картофеля при наилучшем использовании ресурсов, если площадь каждого поля равна 100 га, а картофеля выращено 70 тонн.
г) Картофеля вырастили 50 тонн, а пшеницы – 100 тонн. На сколько в следующем году можно увеличить урожай пшеницы? А картофеля?
Ответ: а) 0,2 т. пшеницы; 1 т. пшеницы; б) 50 т. картофеля; в) картофель – 1 т/га, пшеница – 0,815 т/га; г) пшеница – на 10 тонн, картофель – на 50 тонн.
Задача 17.
Иван может получить на своем поле либо 400 тонн пшеницы, либо 1000 тонн картофеля. Для Петра альтернативной стоимостью выращивания одной тонны картофеля будет производство 0,25 тонн пшеницы при максимальном урожае картофеля, равном 1200 тонн. Два фермера – Иван и Пётр – решили объединить свои усилия. Это не увеличит их производительности.
а) Построить КПВ «коллективного» хозяйства.
б) Верно ли, что альтернативной стоимостью производства первых 1000 тонн картофеля является производство 400 тонн пшеницы?
в) Верно ли, что нельзя произвести 550 тонн пшеницы и 600 тонн картофеля?
г) Верно ли, что при производстве 1700 тонн картофеля альтернативной стоимостью увеличения производства картофеля на 20 тонн является отказ от 8 тонн пшеницы?
д) Верно ли, что для увеличения производства пшеницы с 200 тонн на 550 тонн нужно пожертвовать снижением урожая картофеля на 1100 тонн?
Ответ: правильные утверждения – г, д.
Задача 17.
На одном поле фермер произвести 500 тонн картофеля или 100 тонн пшеницы, а на другом альтернативная стоимость выращивания 2 тонн пшеницы равна 5 тоннам картофеля при максимальном производстве картофеля, равном 1000 тонн. Фермеру необходимо собрать ровно 200 тонн пшеницы. Каково при этом максимально возможное производство картофеля (в тоннах)?
Источник