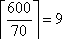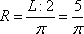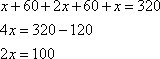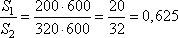Сколько процентов составляет площадь отведенная под грядки от площади всего участка под теплицу
Сергей Петрович решил построить на, дачном участке теплицу длиной 6 м. Для этого он сделал прямоугольный фундамент. Для каркаса теплицы Сергей Петрович заказал металлические дуги в форме полуокружностей длиной 5 м каждая и покрытие для обтяжки.
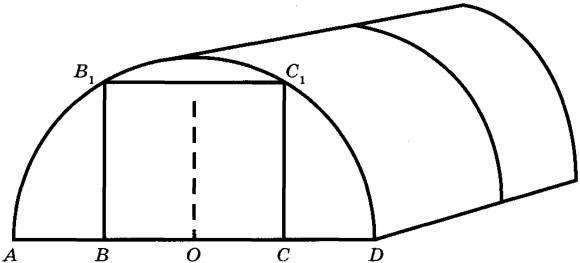
Отдельно требуется купить плёнку для передней и задней стенок теплицы. В передней стенке планируется вход, показанный на рисунке прямоугольником BCC1B1, где точки В, О и С делят отрезок AD на четыре равные части. Внутри теплицы Сергей Петрович планирует сделать три грядки по длине теплицы — одну центральную широкую грядку и две узкие грядки по краям. Между грядками будут дорожки шириной 60 см, для которых необходимо купить тротуарную плитку размером 20 см х 20 см.
Задание 1. Какое наименьшее количество дуг нужно заказать, чтобы расстояние между соседними дугами было не более 70 см?
Вся длина теплицы составляет 6 м = 600 см. Разделим эту длину на 70 см и округлим результат до ближайшего наибольшего целого, получим:
то есть, нужно заказать 9 дуг + 1 первая дуга = 10 дуг.
Задание 2. Сколько упаковок плитки необходимо купить для дорожек между грядками, если она продаётся в упаковках по 8 штук?
В теплице 3 грядки, между которыми будут дорожки, т.е. всего две дорожки. Длина каждой дорожки равна длине теплицы – 600 см, а ширина – 60 см. Площадь одной дорожки 600∙60 = 36000 см2, а двух – 2∙36000 = 72000 см2. Тротуарная плитка имеет размеры 20х20 см с площадью 400 см2. Следовательно, на дорожки необходимо
72000:400 = 180 плиток
Так как плитки продаются в упаковках по 8 штук, то необходимо купить
упаковки
(здесь 
— округление до ближайшего наибольшего целого).
Задание 3. Найдите ширину входа в теплицу. Ответ дайте в метрах с точностью до десятых.
Ширина теплицы определяется диаметром полуокружности длиной 5 метров. Для вычисления радиуса такой полуокружности можно воспользоваться формулой длины окружности 
. Для полуокружности она будет выглядеть так: 
, откуда
и ширина теплицы, равна:
м
Вход в теплицу – это длина отрезка BC. Так как AB=BO=OC=CD, то BC=D:2=R. Получаем ширину входа
м
Задание 4. Найдите ширину центральной грядки, если она в два раза больше ширины узкой грядки. Ответ дайте в сантиметрах с точностью до десятков.
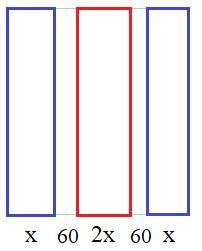
Условно представим теплицу с грядками: две по краям с шириной x см и одна центральная с шириной в 2 раза больше – 2x см. Между ними дорожки шириной 60 см.
Учитывая, что вся ширина теплицы примерно 3,2 м = 320 см, получаем уравнение:
То есть, ширина центральной грядки примерно 100 см.
Задание 5. Сколько процентов составляет площадь, отведённая под грядки, от площади всего участка, отведённого под теплицу? Ответ округлите до целых.
Из рисунка задания 4 видно, что площадь грядок составляет:
см2,
а площадь всей теплицы
см2.
Отношение площадей, равно:
То есть, площадь под грядки составляет 62,5% = 63% от всей площади теплицы.
Источник
Сколько процентов составляет площадь отведенная под грядки от площади всего участка под теплицу
Сергей Петрович решил построить на дачном участке теплицу длиной 6 м. Для этого он сделал прямоугольный фундамент. Для каркаса теплицы Сергей Петрович заказал металлические дуги в форме полуокружностей длиной 6 м каждая и покрытие для обтяжки.
Отдельно требуется купить плёнку для передней и задней стенок теплицы. В передней стенке планируется вход, показанный на рисунке прямоугольником ВСС1В1, где точки B, O и C делят отрезок AD на четыре равные части. Внутри теплицы Сергей Петрович планирует сделать три грядки по длине теплицы — одну центральную широкую грядку и две узкие грядки по краям. Между грядками будут дорожки шириной 60 см, для которых необходимо купить тротуарную плитку размером 20 см х 20 см.
Задание 1. Какое наименьшее количество дуг нужно заказать, чтобы расстояние между соседними дугами было не более 80 см?
Вся длина теплицы составляет 6 м = 600 см. Разделим эту длину на 80 см и округлим результат до ближайшего наибольшего целого, получим:
то есть, нужно заказать 8 дуг + 1 первая дуга = 9 дуг.
Задание 2. Сколько упаковок плитки необходимо купить для дорожек между грядками, если она продаётся в упаковках по 10 штук?
В теплице 3 грядки, между которыми будут дорожки, т.е. всего две дорожки. Длина каждой дорожки равна длине теплицы – 600 см, а ширина – 60 см. Площадь одной дорожки 600∙60 = 36000 см2, а двух – 2∙36000 = 72000 см2. Тротуарная плитка имеет размеры 20х20 см с площадью 400 см2. Следовательно, на дорожки необходимо
72000:400 = 180 плиток
Так как плитки продаются в упаковках по 10 штук, то необходимо купить
180:10 = 18 упаковок
Задание 3. Найдите ширину входа в теплицу. Ответ дайте в метрах с точностью до десятых.
Ширина теплицы определяется диаметром полуокружности длиной 6 метров. Для вычисления радиуса такой полуокружности можно воспользоваться формулой длины окружности 
. Для полуокружности она будет выглядеть так: 
, откуда
и ширина теплицы, равна:
м
Так как AB=BO=OC=CD по условию текста задания, то ширина входа
м
Задание 4. Найдите ширину центральной грядки, если ширина узкой грядки относится к ширине центральной грядки как 3:4. Ответ дайте в сантиметрах с точностью до целых.
Условно представим теплицу с грядками: две по краям с шириной 
см и одна центральная с шириной x см. Между ними дорожки шириной 60 см.
Учитывая, что вся ширина теплицы примерно 3,8 м = 380 см, получаем уравнение:
То есть, ширина центральной грядки примерно 104 см.
Задание 5. Сколько процентов составляет площадь, отведённая под грядки, от площади всего участка, отведённого под теплицу? Ответ округлите до целых.
Площадь, занимаемая грядками, равна:
см2,
а площадь всей теплицы:
см2.
Отношение этих площадей, равно:
,
то есть, грядки занимают примерно 68% от площади всей теплицы.
Источник
Сколько процентов составляет площадь отведенная под грядки от площади всего участка под теплицу
Найдите примерную площадь участка внутри теплицы в квадратных метрах. Ответ округлите до целых.
Алексей Юрьевич решил построить на дачном участке теплицу длиной NP = 4,5 м. Для этого он сделал прямоугольный фундамент. Для каркаса теплицы Алексей Юрьевич заказывает металлические дуги в форме полуокружностей длиной 5,2 м каждая и плёнку для обтяжки. В передней стенке планируется вход, показанный на рисунке прямоугольником ACDB. Точки A и B — середины отрезков MO и ON соответственно.
Какое наименьшее количество дуг нужно заказать, чтобы расстояние между соседними дугами было не более 60 см?
Переведем 60 см = 0,6 м. Найдем количество промежутков между дугами: 4,5 : 0,6 = 7,5, следовательно, наименьшее количество промежутков — 8. Количество дуг на единицу больше, чем количество промежутков: 8 + 1 = 9.
Найдите примерную ширину MN теплицы в метрах. Число π возьмите равным 3,14. Результат округлите до десятых.
Ширина MN представляет собой диаметр окружности. Длина окружности равна 5,2 · 2 = 10,4. Зная о том, что длина окружности может быть вычислена по формуле 
имеем 
Таким образом, D = 3,3.
Сколько квадратных метров плёнки нужно купить для теплицы с учётом передней и задней стенок, включая дверь? Для крепежа плёнку нужно покупать с запасом 10 %. Число π возьмите равным 3,14. Ответ округлите до целых.
Для начала необходимо посчитать площадь крыши теплицы. Крыша представляет собой прямоугольник со сторонами, равными 4,5 м и 5,2 м. Вычислим его площадь: S = 4,5 · 5,2 = 23,4 м 2 . Передняя и задняя стенка — это два полукруга, то есть вместе они составляют круг. Найдем площадь круга: 
(заметим, что в данной формуле l — это не длина окружности, а длина дуги теплицы, то есть половина дуги окружности). Поскольку плёнки надо купить с запасом, прибавляем по 10% к уже имеющимся значениям. Получаем: 
Округляя до целых, получаем 35.
Примечание Решу ОГЭ.
Мы не знаем, как можно купить круглую плёнку для передней и задней частей теплицы (мы бы купили прямоугольную пленку и разрезали её), но за правдивость условий полностью отвечает составитель задачи. Возможно, это задание о других временах или странах.
Источник
Задание 1-5 вариант 19 ОГЭ 2021 из 36 вариантов
Задание 1-5 вариант 19 ОГЭ 2021 из 36 вариантов
Просмотр содержимого документа
«Задание 1-5 вариант 19 ОГЭ 2021 из 36 вариантов»
Задание 1-5 вариант 19 ОГЭ 2021 из 36 вариантов
Сергей Петрович решил построить на, дачном участке теплицу длиной 6 м. Для этого он сделал прямоугольный фундамент. Для каркаса теплицы Сергей Петрович заказал металлические дуги в форме полуокружностей длиной 5 м каждая и покрытие для обтяжки.
Отдельно требуется купить плёнку для передней и задней стенок теплицы. В передней стенке планируется вход, показанный на рисунке прямоугольником BCC1B1, где точки В, О и С делят отрезок AD на четыре равные части. Внутри теплицы Сергей Петрович планирует сделать три грядки по длине теплицы — одну центральную широкую грядку и две узкие грядки по краям. Между грядками будут дорожки шириной 60 см, для которых необходимо купить тротуарную плитку размером 20 см х 20 см.
Задание 1. Какое наименьшее количество дуг нужно заказать, чтобы расстояние между соседними дугами было не более 70 см?
Вся длина теплицы составляет 6 м = 600 см. Разделим эту длину на 70 см и округлим результат до ближайшего наибольшего целого, получим:
то есть, нужно заказать 9 дуг + 1 первая дуга = 10 дуг.
Задание 2. Сколько упаковок плитки необходимо купить для дорожек между грядками, если она продаётся в упаковках по 8 штук?
В теплице 3 грядки, между которыми будут дорожки, т.е. всего две дорожки. Длина каждой дорожки равна длине теплицы – 600 см, а ширина – 60 см. Площадь одной дорожки 600∙60 = 36000 см2, а двух – 2∙36000 = 72000 см2. Тротуарная плитка имеет размеры 20х20 см с площадью 400 см2. Следовательно, на дорожки необходимо
72000:400 = 180 плиток
Так как плитки продаются в упаковках по 8 штук, то необходимо купить
упаковки
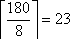
(здесь 
— округление до ближайшего наибольшего целого).
Задание 3. Найдите ширину входа в теплицу. Ответ дайте в метрах с точностью до десятых.
Ширина теплицы определяется диаметром полуокружности длиной 5 метров. Для вычисления радиуса такой полуокружности можно воспользоваться формулой длины окружности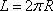 
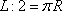
. Для полуокружности она будет выглядеть так: 
, откуда
и ширина теплицы, равна:
м
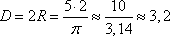
Вход в теплицу – это длина отрезка BC. Так как AB=BO=OC=CD, то BC=D:2=R. Получаем ширину входа
м
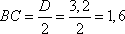
Задание 4. Найдите ширину центральной грядки, если она в два раза больше ширины узкой грядки. Ответ дайте в сантиметрах с точностью до десятков.
Условно представим теплицу с грядками: две по краям с шириной x см и одна центральная с шириной в 2 раза больше – 2x см. Между ними дорожки шириной 60 см.
Учитывая, что вся ширина теплицы примерно 3,2 м = 320 см, получаем уравнение:
То есть, ширина центральной грядки примерно 100 см.
Задание 5. Сколько процентов составляет площадь, отведённая под грядки, от площади всего участка, отведённого под теплицу? Ответ округлите до целых.
Из рисунка задания 4 видно, что площадь грядок составляет:
см2,
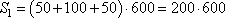
а площадь всей теплицы
см2.
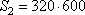
Отношение площадей, равно:
То есть, площадь под грядки составляет 62,5% = 63% от всей площади теплицы.
Источник